题目内容
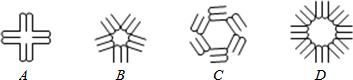
如图,有四张背面相同的纸片A、B、C、D,其正面分别画有四种不同的图案.小红将这四张纸片背面朝上洗匀后随机摸出一张,则摸出的图形是中心对称图形的概率是 .

考点:概率公式,中心对称图形
专题:
分析:确定中心对称图形的个数,利用概率公式求解即可.
解答:解:∵四个图形中有A、C、D三个是中心对称图形,
∴摸出对图形是中心对称图形的概率是
,
故答案为:
.
∴摸出对图形是中心对称图形的概率是
| 3 |
| 4 |
故答案为:
| 3 |
| 4 |
点评:此题考查概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=
.
| m |
| n |

练习册系列答案
相关题目
已知二次函数y=a(x-2)2+c(a>0),当自变量x分别取
、3、0时,对应的函数值分别为y1、y2、y3,则y1、y2、y3的大小关系是( )
| 2 |
| A、y1>y2>y3 |
| B、y2>y1>y3 |
| C、y3>y1>y2 |
| D、y3>y2>y1 |
 如图,P是双曲线上一点,阴影部分的面积为3,则此反比例函数的解析式为
如图,P是双曲线上一点,阴影部分的面积为3,则此反比例函数的解析式为 如图,在等边△ABC中,AB=10,D是BC的中点,将△ABD绕点A旋转后得到△ACE,则线段DE的长度为
如图,在等边△ABC中,AB=10,D是BC的中点,将△ABD绕点A旋转后得到△ACE,则线段DE的长度为 如图,△ABC内接于⊙O,BC=12cm,∠A=60°.⊙O的直径为
如图,△ABC内接于⊙O,BC=12cm,∠A=60°.⊙O的直径为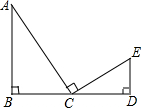 如图,已知AB⊥BD,ED⊥BD,C是线段BD的中点,且AC⊥CE,∠A=30°,那么
如图,已知AB⊥BD,ED⊥BD,C是线段BD的中点,且AC⊥CE,∠A=30°,那么