题目内容
以直角坐标系的原点为圆心作一个半径为5的圆,则以下各点中:J(3,3)、K(1,5)、M(4,3)、N(-1,6),在圆上的点是( )
| A、J | B、K | C、M | D、N |
考点:点与圆的位置关系,坐标与图形性质
专题:
分析:判断一个点是不是在圆内,主要看该点到圆心的距离与半径之间的关系.
解答:解:M(4,3)到圆心的距离都是5=r,故在圆上,
其它点均不在圆上,
故选C.
其它点均不在圆上,
故选C.
点评:本题考查了对点与圆的位置关系的判断.关键要记住若半径为r,点到圆心的距离为d,则有:当d>r时,点在圆外;当d=r时,点在圆上,当d<r时,点在圆内.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 某校为了了解九年级500名学生的体能情况,随机抽查了其中的30名学生,测试了1分钟仰卧起座的次数,并绘制成如图所示的频数分布直方图,请你根据图示计算,估计仰卧起座次数在15~20之间的学生有( )
某校为了了解九年级500名学生的体能情况,随机抽查了其中的30名学生,测试了1分钟仰卧起座的次数,并绘制成如图所示的频数分布直方图,请你根据图示计算,估计仰卧起座次数在15~20之间的学生有( )| A、50 | B、85 |
| C、165 | D、200 |
函数中y=
自变量x的取值范围是( )
| x-2 |
| A、x≥2 | B、x>2 |
| C、x≠2 | D、x≥-2 |
 如图,直线a、b都与直线c相交,下列条件中,能判断a∥b的条件是( )
如图,直线a、b都与直线c相交,下列条件中,能判断a∥b的条件是( )①∠1=∠2 ②∠3=∠6 ③∠2=∠8 ④∠5+∠8=180°.
| A、①③ | B、①②④ |
| C、①③④ | D、②③④ |
已知二次函数y=a(x-2)2+c(a>0),当自变量x分别取
、3、0时,对应的函数值分别为y1、y2、y3,则y1、y2、y3的大小关系是( )
| 2 |
| A、y1>y2>y3 |
| B、y2>y1>y3 |
| C、y3>y1>y2 |
| D、y3>y2>y1 |
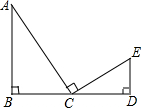 如图,已知AB⊥BD,ED⊥BD,C是线段BD的中点,且AC⊥CE,∠A=30°,那么
如图,已知AB⊥BD,ED⊥BD,C是线段BD的中点,且AC⊥CE,∠A=30°,那么