题目内容
5.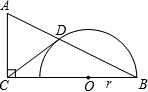 如图,在Rt△ABC中,已知∠ACB=90°,O为BC边上一点,以O为圆心,OB为半径作半圆与AB边交于点D,连结CD,恰好AC=DC.
如图,在Rt△ABC中,已知∠ACB=90°,O为BC边上一点,以O为圆心,OB为半径作半圆与AB边交于点D,连结CD,恰好AC=DC.(1)求证:CD是⊙O的切线;
(2)若AC=3,BC=5,求⊙O的半径r.
分析 (1)连接OD,由等腰三角形的性质得出∠A=∠ADC,∠B=∠ODB,由∠A+∠B=90°,得出∠ADC+∠ODB=90°,因此∠ODC=90°,即可得出结论;
(2)由勾股定理得出方程,解方程即可.
解答 (1)证明:连接OD,如图所示: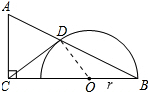 ∵AC=DC,OD=OB,
∵AC=DC,OD=OB,
∴∠A=∠ADC,∠B=∠ODB,
∵∠ACB=90°,
∴∠A+∠B=90°,
∴∠ADC+∠ODB=90°,
∴∠ODC=90°,
即CD⊥OD,
∴CD是⊙O的切线;
(2)解:∵AC=3,BC=5,
∴CD=3,OB=OD=r,OC=5-r,
∵∠ODC=90°,
∴CD2+OD2=OC2,
即32+r2=(5-r)2,
解得:r=1.6;
即⊙O的半径r=1.6.
点评 本题考查了切线的判定、等腰三角形的性质、勾股定理;熟练掌握切线的判定方法,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
20.在直角三角形ABC中,已知∠C=90°,∠A=30°,BC=2,则AC=( )
| A. | 3 | B. | 2$\sqrt{3}$ | C. | 1 | D. | $\frac{\sqrt{3}}{2}$ |
14.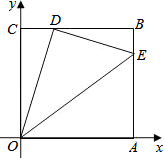 如图,边长为1的正方形OABC的顶点O为坐标原点,点A在x轴的正半轴上,点C在y轴的正半轴上,动点D在边BC上移动(不与点B,C重合),连接OD,过点D作DE⊥OD,交边AB于点E,连接OE,当线段OE的长度取得最小值时,点E的纵坐标为( )
如图,边长为1的正方形OABC的顶点O为坐标原点,点A在x轴的正半轴上,点C在y轴的正半轴上,动点D在边BC上移动(不与点B,C重合),连接OD,过点D作DE⊥OD,交边AB于点E,连接OE,当线段OE的长度取得最小值时,点E的纵坐标为( )
 如图,边长为1的正方形OABC的顶点O为坐标原点,点A在x轴的正半轴上,点C在y轴的正半轴上,动点D在边BC上移动(不与点B,C重合),连接OD,过点D作DE⊥OD,交边AB于点E,连接OE,当线段OE的长度取得最小值时,点E的纵坐标为( )
如图,边长为1的正方形OABC的顶点O为坐标原点,点A在x轴的正半轴上,点C在y轴的正半轴上,动点D在边BC上移动(不与点B,C重合),连接OD,过点D作DE⊥OD,交边AB于点E,连接OE,当线段OE的长度取得最小值时,点E的纵坐标为( )| A. | 0 | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
 如图,反比例函数y=$\frac{k}{x}$的图象经过矩形AOBC的边AC的中点E,与另一边BC交于点D,连接DE,若S△ECD=2,则k的值为( )
如图,反比例函数y=$\frac{k}{x}$的图象经过矩形AOBC的边AC的中点E,与另一边BC交于点D,连接DE,若S△ECD=2,则k的值为( ) 如图,已知l3∥l4∥l5,它们依次交直线l1、l2于点E、A、C和点D、A、B,如果AD=2,AE=3,AB=4,那么CE=9.
如图,已知l3∥l4∥l5,它们依次交直线l1、l2于点E、A、C和点D、A、B,如果AD=2,AE=3,AB=4,那么CE=9.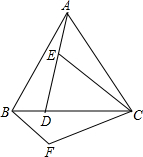 如图,已知△ABC是正三角形,点D是边BC上一点,连接AD,点E是线段AD上一点,连接CE,点F是△ABC外一点,∠CAD=∠CBF,连接BF和CF.
如图,已知△ABC是正三角形,点D是边BC上一点,连接AD,点E是线段AD上一点,连接CE,点F是△ABC外一点,∠CAD=∠CBF,连接BF和CF. 下图是由14个每相邻两点之间距离为1的点组成的“工”字形图形,请仅用无刻度的直尺通过连接图中的点,根据要求画图.
下图是由14个每相邻两点之间距离为1的点组成的“工”字形图形,请仅用无刻度的直尺通过连接图中的点,根据要求画图.