题目内容
20.在直角三角形ABC中,已知∠C=90°,∠A=30°,BC=2,则AC=( )| A. | 3 | B. | 2$\sqrt{3}$ | C. | 1 | D. | $\frac{\sqrt{3}}{2}$ |
分析 先由含30°角的直角三角形的性质得出AB=2BC=4,再根据勾股定理即可求出AC.
解答 解:∵∠C=90°,∠A=30°,BC=2,
∴AB=2BC=4,
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$;
故选:B.
点评 本题考查了含30°角的直角三角形的性质、勾股定理;熟练掌握含30°角的直角三角形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.据成都市气象预报:我市6月份某天中午各县(区)市的气温如表:
则我市各县(区)市这组气温数据的极差是7℃.
| 地名 | 双流 | 仁寿 | 都江堰 | 大邑 | 彭州 | 新都 | 龙泉 |
| 气温 | 37(℃) | 33(℃) | 30(℃) | 31(℃) | 33(℃) | 36(℃) | 34(℃) |
11.若正比例函数y=kx(k≠0)的图象经过点(-2,3),则k的值为( )
| A. | -6 | B. | -$\frac{3}{2}$ | C. | -$\frac{2}{3}$ | D. | 6 |
9.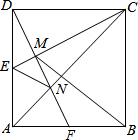 如图,正方形ABCD中,E为AD的中点,DF⊥CE于M,交AC于N,交AB于F,连接EN、BM,有如下结论:①△ADF≌△DCE;②MN=FN;③BM=BC;④S△ADN:S四边形CNFB=2:5;⑤∠ADF=∠BMF.其中正确的结论有( )
如图,正方形ABCD中,E为AD的中点,DF⊥CE于M,交AC于N,交AB于F,连接EN、BM,有如下结论:①△ADF≌△DCE;②MN=FN;③BM=BC;④S△ADN:S四边形CNFB=2:5;⑤∠ADF=∠BMF.其中正确的结论有( )
 如图,正方形ABCD中,E为AD的中点,DF⊥CE于M,交AC于N,交AB于F,连接EN、BM,有如下结论:①△ADF≌△DCE;②MN=FN;③BM=BC;④S△ADN:S四边形CNFB=2:5;⑤∠ADF=∠BMF.其中正确的结论有( )
如图,正方形ABCD中,E为AD的中点,DF⊥CE于M,交AC于N,交AB于F,连接EN、BM,有如下结论:①△ADF≌△DCE;②MN=FN;③BM=BC;④S△ADN:S四边形CNFB=2:5;⑤∠ADF=∠BMF.其中正确的结论有( )| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
10.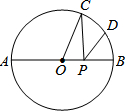 如图,已知⊙O的半径为R,C、D是直径AB的同侧圆周上的两点,弧AC的度数为100°弧BC=2弧BD,动点P在线段AB上,则PC+PD的最小值为( )
如图,已知⊙O的半径为R,C、D是直径AB的同侧圆周上的两点,弧AC的度数为100°弧BC=2弧BD,动点P在线段AB上,则PC+PD的最小值为( )
 如图,已知⊙O的半径为R,C、D是直径AB的同侧圆周上的两点,弧AC的度数为100°弧BC=2弧BD,动点P在线段AB上,则PC+PD的最小值为( )
如图,已知⊙O的半径为R,C、D是直径AB的同侧圆周上的两点,弧AC的度数为100°弧BC=2弧BD,动点P在线段AB上,则PC+PD的最小值为( )| A. | R | B. | $\sqrt{2}$R | C. | $\sqrt{3}$R | D. | $\frac{\sqrt{5}}{2}$R |

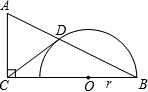 如图,在Rt△ABC中,已知∠ACB=90°,O为BC边上一点,以O为圆心,OB为半径作半圆与AB边交于点D,连结CD,恰好AC=DC.
如图,在Rt△ABC中,已知∠ACB=90°,O为BC边上一点,以O为圆心,OB为半径作半圆与AB边交于点D,连结CD,恰好AC=DC.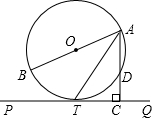 如图,AB为⊙O的直径,D、T是圆上的两点,且AT平分∠BAD,过点T作AD的延长线的垂线PQ,垂足为C.
如图,AB为⊙O的直径,D、T是圆上的两点,且AT平分∠BAD,过点T作AD的延长线的垂线PQ,垂足为C.