Question

17．已知：如图△ABC中，BM、CN是∠ABC、∠ACB的平分线，且AM⊥BM于M，AN⊥CN于N，求证：MN∥BC．

Answer 1

分析 延长AN、AM分别交BC于点D、G，根据BM为∠ABC的角平分线，AM⊥BM得出∠BAM=∠G，故△ABG为等腰三角形，所以BM也为等腰三角形的中线，即AM=GM．同理AN=DN，根据三角形中位线定理即可得出结论．

解答 证明：延长AN、AM分别交BC于点D、G．如图所示：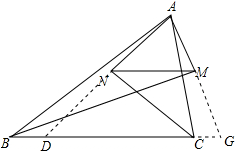
∵BM为∠ABC的角平分线，
∴∠CBM=∠ABM，
∵BM⊥AG，
∴∠ABM+∠BAM=90°，∠G+∠CBM=90°，
∴∠BAM=∠G，
∴△ABG为等腰三角形，
∴BM也为等腰三角形的中线，即AM=GM．
同理AN=DN，
∴MN为△ADG的中位线，
∴MN∥BC．

点评 本题考查了等腰三角形的判定与性质、三角形中位线定理，熟知三角形的中位线平行于第三边，并且等于第三边的一半是解答此题的关键．