题目内容
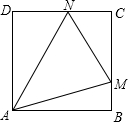如图，正方形ABCD的边长是1，点M，N分别在BC，CD上，使得△CMN的周长为2，则△MAN的面积最小值为考点：正方形的性质,二次函数的最值,全等三角形的判定与性质
专题：几何图形问题
分析：如图，延长CB至L，使BL=DN，则Rt△ABL≌Rt△AND，故AL=AN，进而求证△AMN≌△AML，即可求得∠MAN=∠MAL=45°设CM=x，CN=y，MN=z，根据x2+y2=z2，和x+y+z=2，整理根据△=4（z-2）2-32（1-z）≥0可以解题．
解答：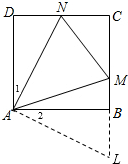
解：延长CB至L，使BL=DN，
则Rt△ABL≌Rt△ADN，
故AL=AN，
∵CM+CN+MN=2，CN+DN+CM+BM=1+1=2，
∴MN=DN+BM=BL+BM=ML，
∴△AMN≌△AML（SSS），
设CM=x，CN=y，MN=z
x2+y2=z2，
∵x+y+z=2，
则x=2-y-z
∴（2-y-z）2+y2=z2，
整理得2y2+（2z-4）y+（4-4z）=0，
∴△=4（z-2）2-32（1-z）≥0，
即（z+2-2
）（z+2+2
）≥0，
又∵z＞0，
∴z≥2
-2
此时S△AMN=S△AML=
ML•AB=
z
因此，当z=2
-2，S△AMN取到最小值为
-1．
故答案为：
-1．
解：延长CB至L，使BL=DN，则Rt△ABL≌Rt△ADN，
故AL=AN，
∵CM+CN+MN=2，CN+DN+CM+BM=1+1=2，
∴MN=DN+BM=BL+BM=ML，
∴△AMN≌△AML（SSS），
设CM=x，CN=y，MN=z
x2+y2=z2，
∵x+y+z=2，
则x=2-y-z
∴（2-y-z）2+y2=z2，
整理得2y2+（2z-4）y+（4-4z）=0，
∴△=4（z-2）2-32（1-z）≥0，
即（z+2-2
| 2 |
| 2 |
又∵z＞0，
∴z≥2
| 2 |
此时S△AMN=S△AML=
| 1 |
| 2 |
| 1 |
| 2 |
因此，当z=2
| 2 |
| 2 |
故答案为：
| 2 |
点评：本题考查了勾股定理在直角三角形中的应用，考查了正方形各边相等，各内角是直角的性质，本题求证三角形全等是解题的关键．
练习册系列答案
相关题目
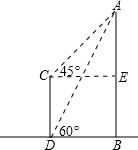某电视塔AB和CD楼的水平距离为200m，从楼顶C处及楼底D处测得塔顶A的仰角分别为45°和60°，试求塔高和楼高（
如图，点A（a，1）、B（-1，b）都在双曲线y=-