题目内容
3.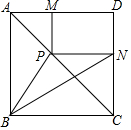 如图,正方形ABCD的对角线上一动点P,作PM⊥AD于点M,PN⊥CD于点N,连接BP,BN,若AB=3,BP=$\sqrt{5}$,则BN的长为( )
如图,正方形ABCD的对角线上一动点P,作PM⊥AD于点M,PN⊥CD于点N,连接BP,BN,若AB=3,BP=$\sqrt{5}$,则BN的长为( )| A. | $\sqrt{15}$ | B. | $\sqrt{13}$或$\sqrt{10}$ | C. | 4 | D. | 5 |
分析 延长NP交AB于H.易知AH=PH,设AH=PH=x,则BH=3-x,在Rt△PBH中,根据PB2=PH2+BH2,可得x2+(3-x)2=($\sqrt{5}$)2,推出x=1或2,接下来分两种情形分别求出BN即可.
解答 解:延长NP交AB于H.
∵四边形ABCD是正方形,
∴∠BAC=90°,AB∥CD,
∵PN⊥CD,
∴PN⊥AB,
∴∠HAP=∠HPA=45°,
∴AH=PH,设AH=PH=x,则BH=3-x,
在Rt△PBH中,∵PB2=PH2+BH2,
∴x2+(3-x)2=($\sqrt{5}$)2,
∴x=1或2,
当x=1时,BH=CN=2,在Rt△BCN中,BN=$\sqrt{B{C}^{2}+C{N}^{2}}$=$\sqrt{{3}^{2}+{2}^{2}}$=$\sqrt{13}$,
当x=2时,BH=CN=1,在Rt△BCN中,BN=$\sqrt{B{C}^{2}+C{N}^{2}}$=,$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$.
综上所述,BN的长为$\sqrt{13}$或$\sqrt{10}$.
故选B.
点评 本题考查正方形的性质、等腰三角形的判定和性质、勾股定理等知识,解题的关键是学会添加常用辅助线面构造直角三角形解决问题,属于中考常考题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.把一张面值10元的人民币兑换成1元或2元的零钱,兑换方案有( )
| A. | 9种 | B. | 8种 | C. | 7种 | D. | 6种 |
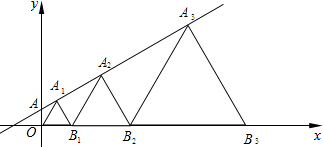 如图,在直线y=$\frac{\sqrt{3}}{3}$x+1上取一点A1,以O、A1为顶点作等一个等边三角形OA1B1,再在直线上取一点A2,以A2、B1为顶点作第二个等边三角形A2B1B2,…,一直这样做下去,则B1点的坐标为($\sqrt{3}$,0),第10个等边三角形的边长为29$\sqrt{3}$.
如图,在直线y=$\frac{\sqrt{3}}{3}$x+1上取一点A1,以O、A1为顶点作等一个等边三角形OA1B1,再在直线上取一点A2,以A2、B1为顶点作第二个等边三角形A2B1B2,…,一直这样做下去,则B1点的坐标为($\sqrt{3}$,0),第10个等边三角形的边长为29$\sqrt{3}$.
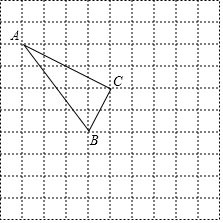 如图,在正方形网格中,每个小正方形的边长为1个单位长度,格点三角形ABC(顶点是网格线的交点的三角形)的顶点A,C的坐标分别为(-4,5),(0,3).
如图,在正方形网格中,每个小正方形的边长为1个单位长度,格点三角形ABC(顶点是网格线的交点的三角形)的顶点A,C的坐标分别为(-4,5),(0,3).