题目内容
18.(1)计算$\sqrt{2}$($\sqrt{2}$+2)-2$\sqrt{2}$+|$\sqrt{3}$-10|,其中$\sqrt{3}$≈1.73.(精确到0.1)(2)解方程组$\left\{\begin{array}{l}{2x-3y=3}\\{3x-2y=7}\end{array}\right.$.
(3)解不等式组:$\left\{\begin{array}{l}{3(x+1)<2x+3}\\{\frac{x-1}{3}≤\frac{x}{2}}\end{array}\right.$,并把解集在数轴上表示出来.
分析 (1)先进行二次根式的乘法运算和去绝对值,然后合并即可;
(2)利用加减消元法解方程组;
(3)分别解两个不等式得到x<0和x≥-2,再利用大小小大中间找确定不等式组的解集,然后利用数轴表示其解集.
解答 解:(1)原式=2+2$\sqrt{2}$-2$\sqrt{2}$+10-$\sqrt{3}$
=12-$\sqrt{3}$
≈10.3;
(2)$\left\{\begin{array}{l}{2x-3y=3①}\\{3x-2y=7②}\end{array}\right.$,
①×2-②×3得-5x=-15,解得x=3,
把x=3代入①得6-3y=3,解得y=1,
所以方程组的解为$\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$;
(3)$\left\{\begin{array}{l}{3(x+1)<2x+3①}\\{\frac{x-1}{3}≤\frac{x}{2}②}\end{array}\right.$,
解①得x<0,
解②得x≥-2,
所以不等式组的解集为-2≤x<0,
用数轴表示为:
点评 本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.也考查了解二元一次方程组和一元一次不等式组.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.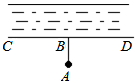 如图,计划把河水引到水池A中,先作AB⊥CD,垂足为B,然后沿AB开渠,能使所开的渠道最短,这样设计的数学根据是( )
如图,计划把河水引到水池A中,先作AB⊥CD,垂足为B,然后沿AB开渠,能使所开的渠道最短,这样设计的数学根据是( )
 如图,计划把河水引到水池A中,先作AB⊥CD,垂足为B,然后沿AB开渠,能使所开的渠道最短,这样设计的数学根据是( )
如图,计划把河水引到水池A中,先作AB⊥CD,垂足为B,然后沿AB开渠,能使所开的渠道最短,这样设计的数学根据是( )| A. | 两点之间,线段最短 | |
| B. | 两条平行线之间的距离处处相等 | |
| C. | 经过直线上或直线外一点,有且只有一条直线与已知直线垂直 | |
| D. | 直线外一点与直线上各点连接的所有线段中,垂线段最短 |
6.以下列各组长度的线段为边,能构成三角形的是( )
| A. | 8,4,4 | B. | 5,6,12 | C. | 6,8,10 | D. | 1,2,3 |
3.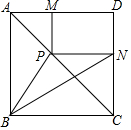 如图,正方形ABCD的对角线上一动点P,作PM⊥AD于点M,PN⊥CD于点N,连接BP,BN,若AB=3,BP=$\sqrt{5}$,则BN的长为( )
如图,正方形ABCD的对角线上一动点P,作PM⊥AD于点M,PN⊥CD于点N,连接BP,BN,若AB=3,BP=$\sqrt{5}$,则BN的长为( )
 如图,正方形ABCD的对角线上一动点P,作PM⊥AD于点M,PN⊥CD于点N,连接BP,BN,若AB=3,BP=$\sqrt{5}$,则BN的长为( )
如图,正方形ABCD的对角线上一动点P,作PM⊥AD于点M,PN⊥CD于点N,连接BP,BN,若AB=3,BP=$\sqrt{5}$,则BN的长为( )| A. | $\sqrt{15}$ | B. | $\sqrt{13}$或$\sqrt{10}$ | C. | 4 | D. | 5 |
10.在菱形ABCD中,若AB=2,则菱形的周长为( )
| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
7.下列运算,正确的是( )
| A. | a2+a2=a4 | B. | a-2=-a2 | C. | a3•(a3)2=a12 | D. | a8÷a3=a5 |
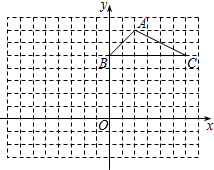 如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶点都在格点上,建立平面直角坐标系,
如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶点都在格点上,建立平面直角坐标系, 如图,水平的讲台上放置的圆柱形笔筒和正方体形粉笔盒,其俯视图是( )
如图,水平的讲台上放置的圆柱形笔筒和正方体形粉笔盒,其俯视图是( )


