题目内容
5.△ABC中,AB=AC,AB的垂直平分线交AB于点N,交BC或其延长线于点M.(1)如图①,当∠A=40°,求∠NMB的大小;
(2)如图②,当∠A=70°,求∠NMB的大小;
(3)写出你由①②发现的规律,并利用图③证明.

分析 (1)根据等腰三角形的性质和三角形内角和定理求出∠B,求出∠MNB=90°,根据三角形内角和定理得出∠NMB=90°-∠B即可.
(2)根据等腰三角形的性质和三角形内角和定理求出∠B,求出∠MNB=90°,根据三角形内角和定理得出∠NMB=90°-∠B即可.
(3)根据等腰三角形的性质和三角形内角和定理求出∠B,求出∠MNB=90°,根据三角形内角和定理得出∠NMB=90°-∠B即可.
解答 解:(1)∵AB=AC,∠A=40°,
∴∠ABC=∠ACB=$\frac{1}{2}$(180°-∠A)=70°,
∵MN是AB的垂直平分线,
∴∠MNB=90°,
∴∠NMB=90°-∠B=20°.
(2)∵AB=AC,∠A=70°,
∴∠B=∠ACB=$\frac{1}{2}$(180°-∠A)=55°,
∵MN是AB的垂直平分线,
∴∠MNB=90°,
∴∠NMB=90°-∠B=35°.
(3)∠NMB=$\frac{1}{2}$∠A,
理由是:∵AB=AC,
∴∠B=∠ACB=$\frac{1}{2}$(180°-∠A)=90°-$\frac{1}{2}$∠A,
∵MN是AB的垂直平分线,
∴∠MNB=90°,
∴∠NMB=90°-∠B=90°-(90°-$\frac{1}{2}$∠A)=$\frac{1}{2}$∠A.
点评 本题考查了等腰三角形的性质,三角形内角和定理和线段垂直平分线性质的应用,主要考查学生的推理能力,求解过程类似.

练习册系列答案
相关题目
20.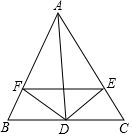 如图,△ABC中,∠A的平分线交BC于D,过点D作DE⊥AC,DF⊥AB,垂足为点E、F,下面四个结论中:①∠AEF=∠AFE;②AD垂直平分EF;③S△BFD:S△CED=BF:CE;④EF∥BC,正确的是( )
如图,△ABC中,∠A的平分线交BC于D,过点D作DE⊥AC,DF⊥AB,垂足为点E、F,下面四个结论中:①∠AEF=∠AFE;②AD垂直平分EF;③S△BFD:S△CED=BF:CE;④EF∥BC,正确的是( )
 如图,△ABC中,∠A的平分线交BC于D,过点D作DE⊥AC,DF⊥AB,垂足为点E、F,下面四个结论中:①∠AEF=∠AFE;②AD垂直平分EF;③S△BFD:S△CED=BF:CE;④EF∥BC,正确的是( )
如图,△ABC中,∠A的平分线交BC于D,过点D作DE⊥AC,DF⊥AB,垂足为点E、F,下面四个结论中:①∠AEF=∠AFE;②AD垂直平分EF;③S△BFD:S△CED=BF:CE;④EF∥BC,正确的是( )| A. | ①②③ | B. | ①③④ | C. | ①②④ | D. | ②③④ |
15.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
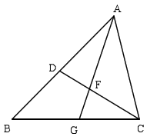 已知:如图,在△ABC中,点D、G分别在边AB、BC上,∠ACD=∠B,AG与CD相交于点F.
已知:如图,在△ABC中,点D、G分别在边AB、BC上,∠ACD=∠B,AG与CD相交于点F. 如图,小正方形的边长均为1,则图中三角形(阴影部分)与△ABC相似的是( )
如图,小正方形的边长均为1,则图中三角形(阴影部分)与△ABC相似的是( )