题目内容
14．
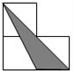如图，小正方形的边长均为1，则图中三角形（阴影部分）与△ABC相似的是（ ）| A． |  | B． |  | C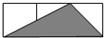． |  | D． |  |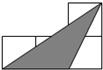
分析 利用△ABC中，∠ACB=135°，AC=2，BC=$\sqrt{2}$，然后根据两组对应边的比相等且夹角对应相等的两个三角形相似可对各选项进行判定．
解答 解：在△ABC中，∠ACB=135°，AC=2，BC=$\sqrt{2}$，
在A、C、D选项中的三角形都没有135°，而在B选项中，三角形的钝角为135°，它的两边分别为1和$\sqrt{2}$，
因为$\frac{2}{\sqrt{2}}$=$\frac{\sqrt{2}}{1}$，所以B选项中的三角形与△ABC相似．
故选B．
点评 本题考查了相似三角形的判定：两组对应边的比相等且夹角对应相等的两个三角形相似；有两组角对应相等的两个三角形相似．
练习册系列答案
名校课堂系列答案
相关题目
△ABC中，AB=AC，三条高AD，BE，CF相交于O，那么图中全等的三角形有7对．
19．
如图所示，函数y=kx与函数 y=$\frac{12}{x}$交于A、B两点，过点A作AE⊥x轴于点E，AE=4，则B点的坐标为（ ）
如图所示，函数y=kx与函数 y=$\frac{12}{x}$交于A、B两点，过点A作AE⊥x轴于点E，AE=4，则B点的坐标为（ ）| A． | （4，-3） | B． | （3，4） | C． | （-3，-4） | D． | （4，3） |
6．下列各组式子中，两个单项式是同类项的是（ ）
| A． | 2a与a2 | B． | xy2与x2y | C． | 5a2b与a2b | D． | 0.3mn2与0.3my2 |
