题目内容
 一个污水处理池,有甲、乙、丙三个水管每个水管,每个水管只能流进污水或流出净水.如图,是污水处理池存水量y(吨)与净水时间x(小时)之间的函数图象,其中AB段只有甲、乙工作,BC段只有甲、丙工作,CD段只有乙、丙工作.
一个污水处理池,有甲、乙、丙三个水管每个水管,每个水管只能流进污水或流出净水.如图,是污水处理池存水量y(吨)与净水时间x(小时)之间的函数图象,其中AB段只有甲、乙工作,BC段只有甲、丙工作,CD段只有乙、丙工作.(1)AB、BC、CD段图象所表达的实际意思是什么?
(2)求40分钟时该污水处理池存水量;
(3)甲、乙、丙三个水管谁是进水管?谁是出水管?三个水管的水流量各是多少?
考点:一次函数的应用
专题:应用题
分析:(1)根据函数的增减性质求解;
(2)先利用待定系数法确定AB的解析式为y=-5x+5(0≤x≤1),然后求自变量为
=
时的函数值;
(3)根据污水处理池存水量的变化得到甲、丙是进水管,乙是出水管,设甲、乙、丙三个水管的水流量分别为x吨/时、y吨/时、z吨/时,列三元一次方程组
,然后解方程组即可.
(2)先利用待定系数法确定AB的解析式为y=-5x+5(0≤x≤1),然后求自变量为
| 40 |
| 60 |
| 2 |
| 3 |
(3)根据污水处理池存水量的变化得到甲、丙是进水管,乙是出水管,设甲、乙、丙三个水管的水流量分别为x吨/时、y吨/时、z吨/时,列三元一次方程组
|
解答:解:(1)AB段图象所表达的实际意思是开始1小时,流出净水比流进污水快,污水处理池存水量由5吨减小到0;BC段图象所表达的实际意思是从1时到2时,污水处理池存水量由0增加到30吨;CD段图象所表达的实际意思是2时到4时,污水处理池存水量由30吨增加到40吨;
(2)设直线AB的解析式为y=kx+b(0≤x≤1),
把A(0,5)、B(1,0)代入得
,解得
,
所以AB的解析式为y=-5x+5(0≤x≤1),
当x=
=
时,y=-5x+5=
,
所以40分钟时该污水处理池存水量为
吨;
(3)甲、乙、丙三个水管中甲、丙是进水管,乙是出水管,
设甲、乙、丙三个水管的水流量分别为x吨/时、y吨/时、z吨/时,
根据题意得
,解得
,
所以甲、乙、丙三个水管的水流量分别为10吨/时、15吨/时、20吨/时.
(2)设直线AB的解析式为y=kx+b(0≤x≤1),
把A(0,5)、B(1,0)代入得
|
|
所以AB的解析式为y=-5x+5(0≤x≤1),
当x=
| 40 |
| 60 |
| 2 |
| 3 |
| 5 |
| 3 |
所以40分钟时该污水处理池存水量为
| 5 |
| 3 |
(3)甲、乙、丙三个水管中甲、丙是进水管,乙是出水管,
设甲、乙、丙三个水管的水流量分别为x吨/时、y吨/时、z吨/时,
根据题意得
|
|
所以甲、乙、丙三个水管的水流量分别为10吨/时、15吨/时、20吨/时.
点评:本题考查了一次函数的应用:从一次函数图象中得到实际问题中的数量关系,再根据有关的数学公式解决实际问题.对于分段函数问题,分段函数是在不同区间有不同对应方式的函数,要特别注意自变量取值范围的划分,既要科学合理,又要符合实际.

练习册系列答案
相关题目
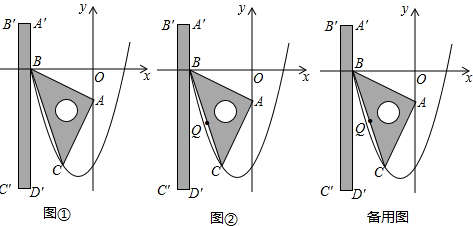
 如图,把抛物线y=
如图,把抛物线y= 如图,直线y=kx+b过A(-1,2)、B(-2,0)两点,则0≤kx+b≤-2x的解集为
如图,直线y=kx+b过A(-1,2)、B(-2,0)两点,则0≤kx+b≤-2x的解集为