题目内容
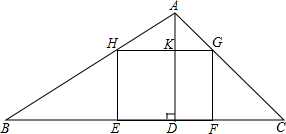如图，△ABC中，BC=24cm，高AD=12cm，矩形EFGH的两个顶点E、F在BC上，另两个顶点G、H分别在AC、AB上，且EF：EH=4：3，求EF、EH的长．考点：相似三角形的判定与性质,矩形的性质
专题：
分析：如图，证明△AGH∽△ACB，运用相似三角形的性质列出比例式，问题即可解决．
解答：解：∵EF：EH=4：3，
∴设EF=4λ，则EH=3λ；
由题意得：
HG∥BC，KD=EH=3λ，HG=EF=4λ；
∴△AGH∽△ACB，而AD⊥BC，AK⊥HG，
∴
=
，即
=
，
解得：λ=
，
∴EF=4λ=
，EH=3λ=
．
∴设EF=4λ，则EH=3λ；
由题意得：
HG∥BC，KD=EH=3λ，HG=EF=4λ；
∴△AGH∽△ACB，而AD⊥BC，AK⊥HG，
∴
| HG |
| BC |
| AK |
| AD |
| 4λ |
| 24 |
| 12-3λ |
| 12 |
解得：λ=
| 12 |
| 5 |
∴EF=4λ=
| 48 |
| 5 |
| 36 |
| 5 |
点评：该题考查了相似三角形的判定及其性质的应用问题；解题的关键是灵活运用有关定理来分析、判断、推理或解答．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
如图，一张矩形纸片ABCD，按图示加以折叠，使得顶点C落在AB边上的E处，若AD=6，则折痕DF的长为（ ）| A、7 | ||
B、7
| ||
| C、8 | ||
D、8
|
一座圆弧形拱桥如图，圆弧形桥拱的跨度AB=12米，C为桥拱的中点，拱高CD=4米，求拱桥的半径．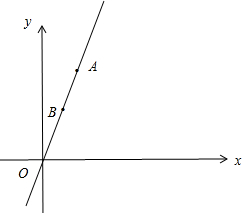
在如图所示的平面直角坐标系中，直线OA的解析式为y=
如图，在四边形ACDE中，AE⊥AC于A，BF⊥AC于B，CD⊥AC于C，若AE=1.5m，BF=3.2m，AB=3m，BC=9m．求CD的长．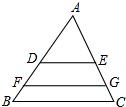
如图，△ABC中，BC=15，DE∥FG∥BC且将△ABC面积三等分，则DE+FG=
已知一次函数y=-kx+k的图象如图，则二次函数y=-kx2-2x+k的图象大致是（ ）
