题目内容
如图，在四边形ACDE中，AE⊥AC于A，BF⊥AC于B，CD⊥AC于C，若AE=1.5m，BF=3.2m，AB=3m，BC=9m．求CD的长．考点：相似三角形的判定与性质
专题：
分析：延长DE、CA交于点G，AE∥BF，可得
=
，结合GB=AG+AB，可求得GA，则可求得GC，再利用AE∥CD可得
=
，代入可求得CD．
| GA |
| GB |
| AE |
| BF |
| GA |
| GC |
| AE |
| CD |
解答：
解：延长DE、CA交于点G，
∵AE∥BF，
∴
=
，且GB=AG+AB，
∴
=
，
解得GA=
，
∴GC=GA+AB+BC=
，
∵AE∥CD，
∴
=
，
∴
=
，
解得CD=8.3m．
解：延长DE、CA交于点G，∵AE∥BF，
∴
| GA |
| GB |
| AE |
| BF |
∴
| GA |
| GA+3 |
| 1.5 |
| 3.2 |
解得GA=
| 45 |
| 17 |
∴GC=GA+AB+BC=
| 249 |
| 17 |
∵AE∥CD，
∴
| GA |
| GC |
| AE |
| CD |
∴
| ||
|
| 1.5 |
| CD |
解得CD=8.3m．
点评：本题主要考查平行线分线段成比例，构造三角形利用平行线分线段成比例求得GA的长是解题的关键．
练习册系列答案
备战中考寒假系列答案
相关题目
二次函数y=ax2+bx+c图象如图，下列正确的个数为（ ）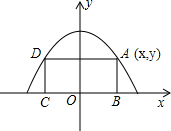
如图，矩形ABCD的顶点B，C在x轴上，A，D在抛物线y=-
如图，直线yy1=x-1与直线y2=-
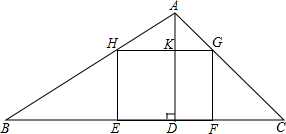如图，△ABC中，BC=24cm，高AD=12cm，矩形EFGH的两个顶点E、F在BC上，另两个顶点G、H分别在AC、AB上，且EF：EH=4：3，求EF、EH的长．
如图，已知△ABC，用直尺和圆规画出一条线段a，使a=AC+BC，然后比较a与AB的长短．