题目内容
 如图,一张矩形纸片ABCD,按图示加以折叠,使得顶点C落在AB边上的E处,若AD=6,则折痕DF的长为( )
如图,一张矩形纸片ABCD,按图示加以折叠,使得顶点C落在AB边上的E处,若AD=6,则折痕DF的长为( )| A、7 | ||
B、7
| ||
| C、8 | ||
D、8
|
考点:翻折变换(折叠问题)
专题:
分析:首先证明△ADE∽△BEF,列出关于线段EF的比例关系式,然后用λ表示出其它线段的长,求出λ问题即可解决.
解答: 解:由题意得:∠DEF=∠C=90°,而∠A=∠B=90°,
解:由题意得:∠DEF=∠C=90°,而∠A=∠B=90°,
∴∠AED+∠ADE=∠AED+∠BEF=90°,
∴∠AED=∠BEF,而∠A=∠B,
∴
=
;由题意得:
BC=AD=6,EF=CF=λ,
∴BF=6-λ;
∵∠ADE=90°-2×30°=30°,且AD=6,
∴cos30°=
,
∴DE=4
,AE=2
,
∴
=
,
解得:λ=4,
∴DF=2λ=8.
故选C.
 解:由题意得:∠DEF=∠C=90°,而∠A=∠B=90°,
解:由题意得:∠DEF=∠C=90°,而∠A=∠B=90°,∴∠AED+∠ADE=∠AED+∠BEF=90°,
∴∠AED=∠BEF,而∠A=∠B,
∴
| DE |
| EF |
| AE |
| BF |
BC=AD=6,EF=CF=λ,
∴BF=6-λ;
∵∠ADE=90°-2×30°=30°,且AD=6,
∴cos30°=
| AD |
| DE |
∴DE=4
| 3 |
| 3 |
∴
4
| ||
| λ |
2
| ||
| 6-λ |
解得:λ=4,
∴DF=2λ=8.
故选C.
点评:该题主要考查了翻折变换的性质及其应用问题;解题的关键是深入分析,准确判断,合情推理,科学论证.

练习册系列答案
相关题目
下列各等式中,是一元一次方程的是( )
| A、2x+y=0 |
| B、x=10 |
| C、1+m=x |
| D、t2=9? |
方程x2=2x-1的一次项系数是( )
| A、1 | B、-1 | C、-2 | D、2 |
参加一次聚会的每两人都握了一次手,所有人握手10次,则参加聚会的人共有( )人.
| A、4 | B、5 | C、6 | D、7 |
 如图,在△ABC中,∠ACB=90°,AD⊥AB,AD=AB,BE⊥DC,AF⊥AC,求证:CF平分∠ACB.
如图,在△ABC中,∠ACB=90°,AD⊥AB,AD=AB,BE⊥DC,AF⊥AC,求证:CF平分∠ACB.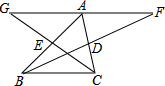 如图,在△ABC中,BD、CE分别是AC、AB边上的中线,分别延长BD、CE到F、G,使DF=BD,EG=CE,则下列结论:①GA=AF,②GA∥BC,③AF∥BC,④G、A、F在一条直线上,⑤A是线段GF的中点,其中正确的有( )
如图,在△ABC中,BD、CE分别是AC、AB边上的中线,分别延长BD、CE到F、G,使DF=BD,EG=CE,则下列结论:①GA=AF,②GA∥BC,③AF∥BC,④G、A、F在一条直线上,⑤A是线段GF的中点,其中正确的有( )
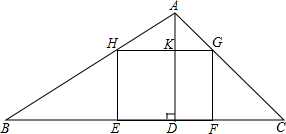 如图,△ABC中,BC=24cm,高AD=12cm,矩形EFGH的两个顶点E、F在BC上,另两个顶点G、H分别在AC、AB上,且EF:EH=4:3,求EF、EH的长.
如图,△ABC中,BC=24cm,高AD=12cm,矩形EFGH的两个顶点E、F在BC上,另两个顶点G、H分别在AC、AB上,且EF:EH=4:3,求EF、EH的长.