题目内容
12.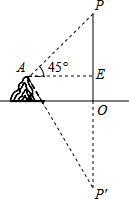 在湖边高出水面50m的山顶A处看见一艘飞艇停留在湖面上空某处,观察到飞艇底部标志P处的仰角为45°,又观其在湖中之像的俯角为60°,则飞艇底部P距离湖面的高度为(参考等式:$\frac{1}{\sqrt{3}-1}$=$\frac{\sqrt{3}+1}{2}$)( )
在湖边高出水面50m的山顶A处看见一艘飞艇停留在湖面上空某处,观察到飞艇底部标志P处的仰角为45°,又观其在湖中之像的俯角为60°,则飞艇底部P距离湖面的高度为(参考等式:$\frac{1}{\sqrt{3}-1}$=$\frac{\sqrt{3}+1}{2}$)( )| A. | 25$\sqrt{3}$+75 | B. | 50$\sqrt{3}$+50 | C. | 75$\sqrt{3}$+75 | D. | 50$\sqrt{3}$+100 |
分析 设AE=x,则PE=AE=x,根据山顶A处高出水面50m,得出OE=50,OP′=x+50,根据∠P′AE=60°,得出P′E=$\sqrt{3}$x,从而列出方程,求出x的值即可.
解答 解:设AE=xm,在Rt△AEP中∠PAE=45°,则∠P=45°,
∴PE=AE=x,
∵山顶A处高出水面50m,
∴OE=50m,
∴OP′=OP=PE+OE=x+50,
∵∠P′AE=60°,
∴P′E=tan60°•AE=$\sqrt{3}$x,
∴OP′=P′E-OE=$\sqrt{3}$x-50,
∴x+50=$\sqrt{3}$x-50,
解得:x=50($\sqrt{3}$+1)(m),
∴PO=PE+OE=50($\sqrt{3}$+1+50=50$\sqrt{3}$+100(m),
即飞艇离开湖面的高度是(50$\sqrt{3}$+100)m.
故选D.
点评 本题考查了解直角三角形的应用-仰角俯角问题,解题的关键是能借助俯角、仰角构造直角三角形并结合图形利用三角函数解直角三角形.

练习册系列答案
相关题目
9.下表记录了甲、乙、丙、丁四名射击运动员最近几次选拔赛成绩的平均数和方差:
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应选择( )
| 甲 | 乙 | 丙 | 丁 | |
| 平均数(环) | 9.14 | 9.15 | 9.14 | 9.15 |
| 方差 | 6.6 | 6.8 | 6.7 | 6.6 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
3.化简x-{-x+[2x-(-x)]}的结果为( )
| A. | -x | B. | x | C. | 5x | D. | -5x |
 如图,利用热气球探测器测量大楼AB的高度,从热气球P处测得大楼B的俯角为37°,大楼底部A的俯角为60°,此时热气球P离底面的高度为120m.试求大楼AB的高度(结果保留整数).
如图,利用热气球探测器测量大楼AB的高度,从热气球P处测得大楼B的俯角为37°,大楼底部A的俯角为60°,此时热气球P离底面的高度为120m.试求大楼AB的高度(结果保留整数).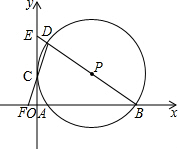 如图,在平面直角坐标系中,⊙P经过y轴上一点C,与x轴分别相交于A、B两点,连接BP并延长分别交⊙P、y轴于点D、E,连接DC并延长交x轴于点F.若点F的坐标为(-1,0),点D的坐标为(1,6).
如图,在平面直角坐标系中,⊙P经过y轴上一点C,与x轴分别相交于A、B两点,连接BP并延长分别交⊙P、y轴于点D、E,连接DC并延长交x轴于点F.若点F的坐标为(-1,0),点D的坐标为(1,6).