题目内容
17.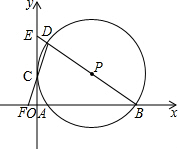 如图,在平面直角坐标系中,⊙P经过y轴上一点C,与x轴分别相交于A、B两点,连接BP并延长分别交⊙P、y轴于点D、E,连接DC并延长交x轴于点F.若点F的坐标为(-1,0),点D的坐标为(1,6).
如图,在平面直角坐标系中,⊙P经过y轴上一点C,与x轴分别相交于A、B两点,连接BP并延长分别交⊙P、y轴于点D、E,连接DC并延长交x轴于点F.若点F的坐标为(-1,0),点D的坐标为(1,6).(1)求证:CD=CF;
(2)判断⊙P与y轴的位置关系,并说明理由;
(3)求直线BD的解析式.
分析 (1)证△COF≌△CHD可得CD=CF;
(2)连接PC,先由CD=CF、PD=PB知PC∥BF,结合BF⊥y轴知PC⊥y轴,即可得出结论;
(3)连接AD,证BD=BF可得AD=OH=6、OA=DH=1,设BD=x,由BD2=AB2+AD2得x=10,从而知B(9,0),待定系数法求解可得.
解答 解:(1)如图,作DH⊥OE于点H,
∴∠DHC=∠FOC=90°,∠DCH=∠FCO,
∵D(1,6)、F(-1,0),
∴DH=OF=1,
在△COF和△CHD中,
∵$\left\{\begin{array}{l}{∠COF=∠CHD}\\{∠OCF=∠HCD}\\{OF=HD}\end{array}\right.$,
∴△COF≌△CHD(AAS),
∴CD=CF;
(2)连接PC,
∵CD=CF、PD=PB,
∴PC为△BDF的中位线,
∴PC∥BF,
∵BF⊥y轴,
∴PC⊥y轴,
又PC为⊙P的半径,
∴⊙P与y轴相切;
(3)如图,连接AD,
由(2)知BF=2PC,
∵BD=2PC,
∴BD=BF,
∵BD是⊙P的直径,
∴∠DAB=90°,
∴AD=OH=6,OA=DH=1,
设BD=x,
则AB=x-2,
由BD2=AB2+AD2得x2=(x-2)2+62,
解得:x=10,
∴OB=OA+AB=1+8=9,即B(9,0),
设直线BD的解析式为y=kx+b,
把B(9,0)、D(1,6)代入得$\left\{\begin{array}{l}{9k+b=0}\\{k+b=6}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{3}{4}}\\{b=\frac{27}{4}}\end{array}\right.$,
∴直线BD的解析式为y=-$\frac{3}{4}$x+$\frac{27}{4}$.
点评 本题考查了圆的综合题.此题难度不大,其中涉及到了待定系数法求一次函数解析式,坐标与图形的性质,全等三角形的判定与性质以及切线的判定与性质.解题时,注意数形结合数学思想的应用.

 阅读快车系列答案
阅读快车系列答案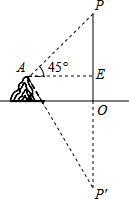 在湖边高出水面50m的山顶A处看见一艘飞艇停留在湖面上空某处,观察到飞艇底部标志P处的仰角为45°,又观其在湖中之像的俯角为60°,则飞艇底部P距离湖面的高度为(参考等式:$\frac{1}{\sqrt{3}-1}$=$\frac{\sqrt{3}+1}{2}$)( )
在湖边高出水面50m的山顶A处看见一艘飞艇停留在湖面上空某处,观察到飞艇底部标志P处的仰角为45°,又观其在湖中之像的俯角为60°,则飞艇底部P距离湖面的高度为(参考等式:$\frac{1}{\sqrt{3}-1}$=$\frac{\sqrt{3}+1}{2}$)( )| A. | 25$\sqrt{3}$+75 | B. | 50$\sqrt{3}$+50 | C. | 75$\sqrt{3}$+75 | D. | 50$\sqrt{3}$+100 |
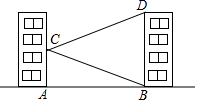 如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口C测得教学楼顶部D的仰角为18°,教学楼底部B的俯角为20°,量得实验楼与教学楼之间的距离AB=30m.
如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口C测得教学楼顶部D的仰角为18°,教学楼底部B的俯角为20°,量得实验楼与教学楼之间的距离AB=30m.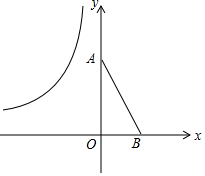 如图,已知原点O,A(0,4),B(2,0),将△OAB绕平面内一点P逆时针旋转90°,使得旋转后的三角形的两个顶点恰好落在双曲线y=$\frac{-6}{x}$(x<0)上,则旋转中心P的坐标为(-$\frac{3}{2}$,-$\frac{1}{2}$).
如图,已知原点O,A(0,4),B(2,0),将△OAB绕平面内一点P逆时针旋转90°,使得旋转后的三角形的两个顶点恰好落在双曲线y=$\frac{-6}{x}$(x<0)上,则旋转中心P的坐标为(-$\frac{3}{2}$,-$\frac{1}{2}$).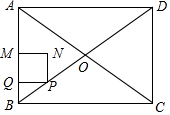 如图,矩形ABCD的对角线相交于点O,AB=6cm,BC=8cm,动点P以1cm/s的速度从点B出发,沿B→O→C向终点C运动,当点P在OB上运动时,过点P作PQ⊥AB于点Q,以PQ为边向上方作正方形PQMN,当点P在OC上运动时,过点P作PQ∥AB交OD于点Q,以PQ为边向左侧作正方形PQMN,设正方形PQMN与△ABO重叠部分图形的面积为S(cm2),点P运动的时间为t(s).
如图,矩形ABCD的对角线相交于点O,AB=6cm,BC=8cm,动点P以1cm/s的速度从点B出发,沿B→O→C向终点C运动,当点P在OB上运动时,过点P作PQ⊥AB于点Q,以PQ为边向上方作正方形PQMN,当点P在OC上运动时,过点P作PQ∥AB交OD于点Q,以PQ为边向左侧作正方形PQMN,设正方形PQMN与△ABO重叠部分图形的面积为S(cm2),点P运动的时间为t(s).
 下面数据是截至2010年费尔兹奖得主获奖时的年龄:
下面数据是截至2010年费尔兹奖得主获奖时的年龄:
