题目内容
9.下表记录了甲、乙、丙、丁四名射击运动员最近几次选拔赛成绩的平均数和方差:| 甲 | 乙 | 丙 | 丁 | |
| 平均数(环) | 9.14 | 9.15 | 9.14 | 9.15 |
| 方差 | 6.6 | 6.8 | 6.7 | 6.6 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
分析 利用平均数和方差的意义进行判断.
解答 解:丁的平均数最大,方差最小,成绩最稳当,
所以选丁运动员参加比赛.
故选D.
点评 本题考查了方差:一组数据中各数据与它们的平均数的差的平方的平均数,叫做这组数据的方差.方差是反映一组数据的波动大小的一个量.方差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
17.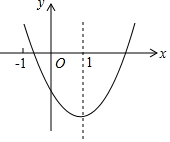 二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,下列结论:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,下列结论:
①ab<0;②b2>4ac;③a+b+2c<0;④3a+c<0.
其中正确的是( )
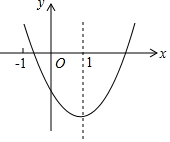 二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,下列结论:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,下列结论:①ab<0;②b2>4ac;③a+b+2c<0;④3a+c<0.
其中正确的是( )
| A. | ①④ | B. | ②④ | C. | ①②③ | D. | ①②③④ |
1.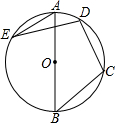 如图,AB是⊙O的直径,点C,D,E在⊙O上,若∠AED=20°,则∠BCD的度数为( )
如图,AB是⊙O的直径,点C,D,E在⊙O上,若∠AED=20°,则∠BCD的度数为( )
 如图,AB是⊙O的直径,点C,D,E在⊙O上,若∠AED=20°,则∠BCD的度数为( )
如图,AB是⊙O的直径,点C,D,E在⊙O上,若∠AED=20°,则∠BCD的度数为( )| A. | 100° | B. | 110° | C. | 115° | D. | 120° |
12.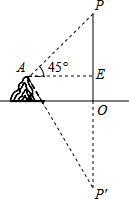 在湖边高出水面50m的山顶A处看见一艘飞艇停留在湖面上空某处,观察到飞艇底部标志P处的仰角为45°,又观其在湖中之像的俯角为60°,则飞艇底部P距离湖面的高度为(参考等式:$\frac{1}{\sqrt{3}-1}$=$\frac{\sqrt{3}+1}{2}$)( )
在湖边高出水面50m的山顶A处看见一艘飞艇停留在湖面上空某处,观察到飞艇底部标志P处的仰角为45°,又观其在湖中之像的俯角为60°,则飞艇底部P距离湖面的高度为(参考等式:$\frac{1}{\sqrt{3}-1}$=$\frac{\sqrt{3}+1}{2}$)( )
 在湖边高出水面50m的山顶A处看见一艘飞艇停留在湖面上空某处,观察到飞艇底部标志P处的仰角为45°,又观其在湖中之像的俯角为60°,则飞艇底部P距离湖面的高度为(参考等式:$\frac{1}{\sqrt{3}-1}$=$\frac{\sqrt{3}+1}{2}$)( )
在湖边高出水面50m的山顶A处看见一艘飞艇停留在湖面上空某处,观察到飞艇底部标志P处的仰角为45°,又观其在湖中之像的俯角为60°,则飞艇底部P距离湖面的高度为(参考等式:$\frac{1}{\sqrt{3}-1}$=$\frac{\sqrt{3}+1}{2}$)( )| A. | 25$\sqrt{3}$+75 | B. | 50$\sqrt{3}$+50 | C. | 75$\sqrt{3}$+75 | D. | 50$\sqrt{3}$+100 |
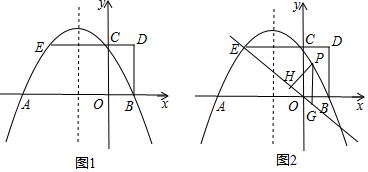
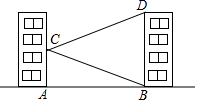 如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口C测得教学楼顶部D的仰角为18°,教学楼底部B的俯角为20°,量得实验楼与教学楼之间的距离AB=30m.
如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口C测得教学楼顶部D的仰角为18°,教学楼底部B的俯角为20°,量得实验楼与教学楼之间的距离AB=30m. 如图,在菱形ABCD中,若AC=6,BD=8,则菱形ABCD的面积是24.
如图,在菱形ABCD中,若AC=6,BD=8,则菱形ABCD的面积是24.