题目内容
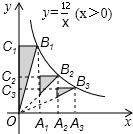 如图所示,点A1,A2,A3在x轴上,且OA1=A1A2=A2A3,分别过点A1,A2,A3作y轴的平行线,与反比例函数y=
如图所示,点A1,A2,A3在x轴上,且OA1=A1A2=A2A3,分别过点A1,A2,A3作y轴的平行线,与反比例函数y=| 12 |
| x |
考点:反比例函数系数k的几何意义
专题:
分析:根据反比例函数上的点向x轴、y轴引垂线形成的矩形面积等于反比例函数的|k|,得到S△OB1C1=S△OB2C2=S△OB3C3=
|k|=6,再根据相似三角形的面积比等于相似比的平方得到3个阴影部分的三角形的面积从而求得面积和.
| 1 |
| 2 |
解答:解:根据题意可知S△OB1C1=S△OB2C2=S△OB3C3=
|k|=6,
∵OA1=A1A2=A2A3,A1B1∥A2B2∥A3B3∥y轴,
设图中阴影部分的面积从左向右依次为s1,s2,s3
则s1=
|k|=6,
∵OA1=A1A2=A2A3,
∴s2:S△OB2C2=1:4,s3:S△OB3C3=1:9,
∴图中阴影部分的面积分别是s1=6,s2=
,s3=
,
∴图中阴影部分的面积之和=6+
+
=8
.
故答案为8
.
| 1 |
| 2 |
∵OA1=A1A2=A2A3,A1B1∥A2B2∥A3B3∥y轴,
设图中阴影部分的面积从左向右依次为s1,s2,s3
则s1=
| 1 |
| 2 |
∵OA1=A1A2=A2A3,
∴s2:S△OB2C2=1:4,s3:S△OB3C3=1:9,
∴图中阴影部分的面积分别是s1=6,s2=
| 3 |
| 2 |
| 2 |
| 3 |
∴图中阴影部分的面积之和=6+
| 3 |
| 2 |
| 2 |
| 3 |
| 1 |
| 6 |
故答案为8
| 1 |
| 6 |
点评:此题综合考查了反比例函数的性质,此题难度稍大,综合性比较强,注意反比例函数上的点向x轴、y轴引垂线形成的矩形面积等于反比例函数的|k|.

练习册系列答案
相关题目
 如图,正方形ABCD的边长为
如图,正方形ABCD的边长为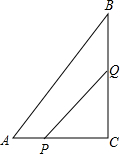 如图,△ABC中,∠C=90°,AC=6cm,BC=8cm,点Q是线段BC的中点,点P从A开始沿AC边向C以1cm/s的速度移动.问:经过几秒钟,四边形APQB的面积是16cm2?
如图,△ABC中,∠C=90°,AC=6cm,BC=8cm,点Q是线段BC的中点,点P从A开始沿AC边向C以1cm/s的速度移动.问:经过几秒钟,四边形APQB的面积是16cm2?