题目内容
8.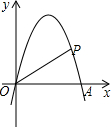 如图,在平面直角坐标系中,抛物线y=-x2+4x与x轴交于点O、A,点P在抛物线上,连结OP、AP,设点P的横坐标为m,△AOP的面积为S,若0<m<3,则S的取值范围是0<S≤8.
如图,在平面直角坐标系中,抛物线y=-x2+4x与x轴交于点O、A,点P在抛物线上,连结OP、AP,设点P的横坐标为m,△AOP的面积为S,若0<m<3,则S的取值范围是0<S≤8.
分析 表示出P点坐标,进而表示出△PAB的底与高的长度,即可得出S与m的关系式,利用配方法可得△PAB的面积S的取值范围.
解答 解:由题意,P点坐标为:(m,-m2+4m),
∵抛物线y=-x2+4x与x轴交于点O、A,
∴当y=0时,-x2+4x=0,
解得:x=0,或x=4,
∴A(4,0),
∴OA=4,
由题意可得:P到AB的距离为-m2+4m,
∴S=$\frac{1}{2}$×4×(-m2+4m)=-2m2+8m=-2(m-2)2+8;
∵0<m<3,
∴0<S≤8.
故答案为:0<S≤8.
点评 此题主要考查了二次函数的综合应用以及三角形面积求法和图象上点的坐标性质,根据P点坐标得出P到AB的距离是解题关键.

练习册系列答案
相关题目
13.下列各图中,能够由∠1=∠2得到AB∥CD的是( )
| A. | 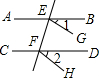 | B. | 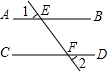 | C. | 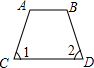 | D. | 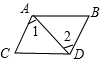 |
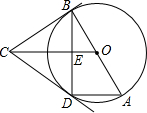 如图,已知AB是⊙O的直径,BC是⊙O的切线,B是切点,⊙O的弦AD∥OC.
如图,已知AB是⊙O的直径,BC是⊙O的切线,B是切点,⊙O的弦AD∥OC.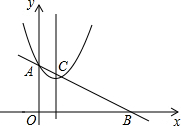 如图,在平面直角坐标系中,抛物线y=x2-2x+2交y轴于点A,直线AB交x轴正半轴于点B,交抛物线的对称轴于点C,若OB=2OA,则点C的坐标为(1,$\frac{3}{2}$).
如图,在平面直角坐标系中,抛物线y=x2-2x+2交y轴于点A,直线AB交x轴正半轴于点B,交抛物线的对称轴于点C,若OB=2OA,则点C的坐标为(1,$\frac{3}{2}$).