题目内容
14.解方程:$\frac{2{x}^{2}+6x}{{x}^{2}+2}$-$\frac{5{x}^{2}+10}{{x}^{2}+3x}$+3=0.分析 根据方程特点设y=$\frac{{x}^{2}+3x}{{x}^{2}+2}$,则原方程可化为2y2+3y-5=0.解一元二次方程求y,再求x.
解答 解:设$\frac{{x}^{2}+3x}{{x}^{2}+2}$=y,则原方程化为2y2+3y-5=0,
解得y1=$\frac{5}{2}$,y2=-1.
当y1=$\frac{5}{2}$时,$\frac{{x}^{2}+3x}{{x}^{2}+2}$=$\frac{5}{2}$,化简,得
3x2-6x+10=0,△=2-4ac=-84<0,方程无解;
当y2=-1时,$\frac{{x}^{2}+3x}{{x}^{2}+2}$=-1.
化简,得2x2+3x+2=0,△=b2-4ac=-7<0,方程无解.
故原方程的根无解.
点评 本题考查了换元法解分式方程,用换元法解一些复杂的分式方程是比较简单的一种方法,根据方程特点设出相应未知数,解方程能够使问题简单化,注意求出方程解后要验根.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
6.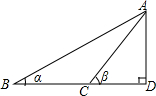 如图所示,已知∠ABD=α.△ACD=β,BC=a,则高AD为( )
如图所示,已知∠ABD=α.△ACD=β,BC=a,则高AD为( )
 如图所示,已知∠ABD=α.△ACD=β,BC=a,则高AD为( )
如图所示,已知∠ABD=α.△ACD=β,BC=a,则高AD为( )| A. | $\frac{tanα•tanβ}{tanβ-tanα}$•a | B. | ($\frac{1}{tanα}$-$\frac{1}{tanβ}$)•a | ||
| C. | $\frac{1}{tanα-tanβ}$•a | D. | (tanα-tanβ)•a |
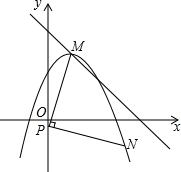 已知,抛物线y=-$\frac{3}{4}$(x-1)2+3顶点为M,点N在抛物线,点P在y轴上,(点M、N、P逆时针方向排列),PN=PM,PN⊥PM,求P点坐标.
已知,抛物线y=-$\frac{3}{4}$(x-1)2+3顶点为M,点N在抛物线,点P在y轴上,(点M、N、P逆时针方向排列),PN=PM,PN⊥PM,求P点坐标.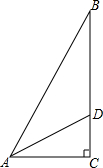 如图,在△ABC中,∠C=90°,∠A的平分线AD=4,∠DAC=30°,解直角△ABC.
如图,在△ABC中,∠C=90°,∠A的平分线AD=4,∠DAC=30°,解直角△ABC.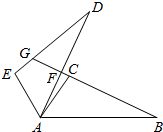 如图,△ABC≌△ADE,∠CAD=10°,∠B=25°,∠EAB=120°,则∠DFB=90°.
如图,△ABC≌△ADE,∠CAD=10°,∠B=25°,∠EAB=120°,则∠DFB=90°.