题目内容
11.△ABC中,BC=18,AC=12,AB=9,点D,E分别是直线AB,AC上的两个点,AE=4.若由A,D,E构成的三角形与△ABC相似,则DB的长为6或$\frac{11}{3}$或12或$\frac{43}{3}$.分析 由A,D,E构成的三角形与△ABC相似,根据相似三角形的对应边成比例,分四种情况讨论,即可求得DB的长.
解答 解:∵由A,D,E构成的三角形与△ABC相似,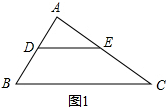
分四种情况:
①当△ADE∽△ABC时,如图1所示
$\frac{AD}{AB}=\frac{AE}{AC}$=$\frac{4}{12}$=$\frac{1}{3}$,
∴AD=$\frac{1}{3}$AB=$\frac{1}{3}$×9=3,
则BD=AB-AD=6;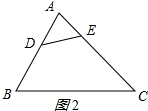 ②△ADE∽△ACB时,如图2所示:
②△ADE∽△ACB时,如图2所示:
$\frac{AD}{AC}=\frac{AE}{AB}$,
∴AD=$\frac{AE•AC}{AB}$=$\frac{4×12}{9}$=$\frac{16}{3}$,
∴BD=AB-AD=9-$\frac{16}{3}$=$\frac{11}{3}$;
③△ADE∽△ABC时,如图3所示: $\frac{AD}{AB}=\frac{AE}{AC}$=$\frac{4}{12}$=$\frac{1}{3}$,
$\frac{AD}{AB}=\frac{AE}{AC}$=$\frac{4}{12}$=$\frac{1}{3}$,
∴AD=$\frac{1}{3}$AB=$\frac{1}{3}$×9=3,
则BD=AB+AD=12;
④△ADE∽△ACB时,如图4所示:
$\frac{AD}{AC}=\frac{AE}{AB}$,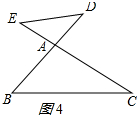 ∴AD=$\frac{AE•AC}{AB}$=$\frac{4×12}{9}$=$\frac{16}{3}$,
∴AD=$\frac{AE•AC}{AB}$=$\frac{4×12}{9}$=$\frac{16}{3}$,
∴BD=AB+AD=9+$\frac{16}{3}$=$\frac{43}{3}$;
综上所述:DB的长为:6或$\frac{11}{3}$或12或$\frac{43}{3}$;
故答案为:6或$\frac{11}{3}$或12或$\frac{43}{3}$.
点评 此题考查了相似三角形的性质.此题难度适中,注意掌握分类讨论思想与数形结合思想的应用.

| A. | 下降6米 | B. | 上升6米 | C. | 下降或上升6米 | D. | 上升-6米 |
| A. | 3 | B. | -3 | C. | ±3 | D. | ±$\frac{1}{3}$ |
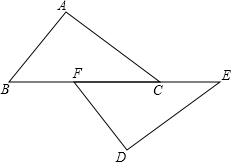 如图,点B、F、C、E在一条直线上,AB=DE,FB=CE,AC=DF,求证:△ABC≌△DEF.
如图,点B、F、C、E在一条直线上,AB=DE,FB=CE,AC=DF,求证:△ABC≌△DEF.