题目内容
1.(1)如图1,点P在⊙O外,PC是⊙O的切线、切点为C,直线PO与⊙O相交于点A、B,求∠P与∠A的数量关系;(2)在(1)的条件下,若∠A=30°,则PB与⊙O的半径有什么关系?
(3)若AB是圆的任意一条直径,C为⊙O上任意一点,连接CA,∠A可能等于45°吗?若∠A=45°,则过点C的切线与AB有怎样的位置关系?
(4)在(3)条件下,若∠A>45°,则过点C的切线与直线AB的交点P的位置将在哪里?
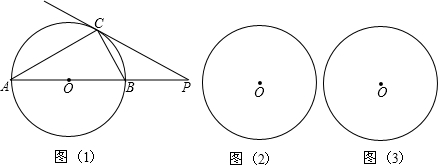
分析 (1)连结OC,如图(1),根据切线的性质得∠OCP=90°,则∠P+∠POC=90°,由于∠A=∠OCA,则∠POC=∠A+∠OCA=2∠A,所以∠P+2∠A=90°;
(2)由(1)得,当∠A=30°时,∠P=30°,利用含30度的直角三角形三边的关系得PO=2OC,则PB=OB,即PB与⊙O的半径相等;
(3)如图(2),点C为半圆AB的中点,PC为⊙O的切线,连结OC,根据圆周角定理得到∠ACB=90°,再利用CA弧=CB弧可得∠A=∠B=45°,则根据等腰三角形的性质得OC⊥AB,然后根据切线的性质得OC⊥PC,
于是可判断PC∥AB,所以当∠A=45°,过点C的切线与AB平行;
(4)当∠A>45°,判断弧AC<弧BC,则过点C的切线与直线AB的交点P在BA的延长线上.
解答 解:(1)连结OC,如图(1),
∵PC是⊙O的切线,
∴OC⊥PC,
∴∠OCP=90°,
∴∠P+∠POC=90°,
∵OC=OA,
∴∠A=∠OCA,
∴∠POC=∠A+∠OCA=2∠A,
∴∠P+2∠A=90°,
即∠P=90°-2∠A;
(2)当∠A=30°时,∠P=90°-2×30°=30°,
∴PO=2OC,
即PB+OB=2OB,
∴PB=OB,
即PB与⊙O的半径相等;
(3)∠A有可能等于45°,如图(2),点C为半圆AB的中点,PC为⊙O的切线,连结OC,
∵AB为直径,
∴∠ACB=90°,
而CA弧=CB弧,
∴∠A=∠B=45°,
∴OC⊥AB,
而PC为切线,
∴OC⊥PC,
∴PC∥AB,
∴当∠A=45°,过点C的切线与AB平行;
(4)如图(3),当∠A>45°,而∠ACB=90°,所以∠CAB>∠B,弧AC<弧BC,则过点C的切线与直线AB的交点P在BA的延长线上.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了圆周角定理和等腰三角形的判定.


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | $\frac{1}{4}$和-0.25互为倒数 | B. | $\frac{1}{4}$和-4互为倒数 | ||
| C. | 0.1和10互为倒数 | D. | 0的倒数是0 |

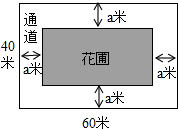 如图,为美化环境,某校计划在一块长为60米,宽为40米的长方形空地上修建一个长方形花圃,并将花圃四周余下的空地修建成同样宽的通道,设通道宽为a米.
如图,为美化环境,某校计划在一块长为60米,宽为40米的长方形空地上修建一个长方形花圃,并将花圃四周余下的空地修建成同样宽的通道,设通道宽为a米.