题目内容
17.探究,观察下列各式:$\frac{1}{1×2}$=1$-\frac{1}{2}$,$\frac{1}{2×3}$=$\frac{1}{2}$$-\frac{1}{3}$,$\frac{1}{3×4}$=$\frac{1}{3}$-$\frac{1}{4}$,…(1)请仿照以上的各式的变形方式,对下列各题进行变形探究:
①$\frac{1}{2×4}$=$\frac{1}{2}$($\frac{1}{2}$-$\frac{1}{4}$);②$\frac{1}{4×6}$=$\frac{1}{2}$($\frac{1}{4}$-$\frac{1}{6}$);③$\frac{1}{98×100}$=$\frac{1}{2}$($\frac{1}{98}$-$\frac{1}{100}$)
(2)已知|x-1|+(y-2)2=0,求$\frac{1}{xy}$+$\frac{1}{(x+1)(y+1)}$+…+$\frac{1}{(x+2008)(y+2008)}$的值.
分析 (1)把各个分数拆项即可求解;
(2)先根据非负数的性质求得x,y,再利用得出的规律化简原式,抵消合并即可得到结果.
解答 解:(1)①$\frac{1}{2×4}$=$\frac{1}{2}$($\frac{1}{2}$-$\frac{1}{4}$);②$\frac{1}{4×6}$=$\frac{1}{2}$($\frac{1}{4}$-$\frac{1}{6}$);③$\frac{1}{98×100}$=$\frac{1}{2}$($\frac{1}{98}$-$\frac{1}{100}$);
(2)∵|x-1|+(y-2)2=0,
∴x-1=0,y-2=0,
解得x=1,y=2,
∴$\frac{1}{xy}$+$\frac{1}{(x+1)(y+1)}$+…+$\frac{1}{(x+2008)(y+2008)}$
=$\frac{1}{1×2}$+$\frac{1}{2×3}$+…+$\frac{1}{2009×2010}$
=1-$\frac{1}{2}$+$\frac{1}{2}$$-\frac{1}{3}$+…+$\frac{1}{2009}$-$\frac{1}{2010}$
=1-$\frac{1}{2010}$
=$\frac{2009}{2010}$.
故答案为:$\frac{1}{2}$($\frac{1}{2}$-$\frac{1}{4}$); $\frac{1}{2}$($\frac{1}{4}$-$\frac{1}{6}$);$\frac{1}{2}$($\frac{1}{98}$-$\frac{1}{100}$).
点评 考查了代数式求值,非负数的性质,在解答中注意观察题目的变化规律,运用规律解答能使运算简便,并且得心应手.

练习册系列答案
相关题目
9.22016×(-2)2016的计算结果是( )
| A. | 0 | B. | -24032 | C. | 24032 | D. | -44032 |
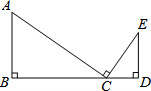 已知:如图,AC⊥CE,AB⊥BD,ED⊥BD,BC=DE,求证:△ABC≌△CDE.
已知:如图,AC⊥CE,AB⊥BD,ED⊥BD,BC=DE,求证:△ABC≌△CDE.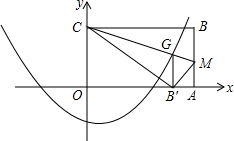 OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴上,点C在y轴上,OA=10,OC=6.
OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴上,点C在y轴上,OA=10,OC=6.