题目内容
2．一件工艺品进价为100元，标价135元售出，每天可售出100件，根据销售统计，一件工艺品每降价1元，则每天可以多售出4件．要使每天获得的利润最大，则每件降价的钱数为5元．分析 设每件需降价的钱数为x元，每天获利y元，则可求出y与x之间的函数关系式，写成顶点式后直接解答．
解答 解：设每件需降价的钱数为x元，每天获利y元，
则y=（135-x-100）（100+4x），
即：y=-4（x-5）2+3600，
∵-4＜0，
∴当x=5元时，每天获得的利润最大．
故答案为：5元．
点评 本题主要考查了二次函数的实际应用，根据每天的利润=一件的利润×销售件数，建立函数关系式，此题为数学建模题，借助二次函数解决实际问题．
练习册系列答案
相关题目
16．某小区改善生态环境，促进生活垃圾的分类处理，将少活垃圾分成三类：厨房垃圾、可回收垃圾和其他垃圾，分别记为m，n，p，并且设置了相应的垃圾箱，“厨房垃圾”箱，“可回收垃圾”箱和“其他垃圾”箱，分别记为A，B，C．
（1）若将三类垃圾随机投入三类垃圾箱，请用画树状图的方法求垃圾投放正确的概率；
（2）为了了解居民生活垃圾分类投放的情况，现随机抽取了小区三类垃圾箱中总共1000吨生活垃圾，数据统计如下（单位：吨）：
请根据以上信息，试估计“厨房垃圾”投放正确的概率．
（1）若将三类垃圾随机投入三类垃圾箱，请用画树状图的方法求垃圾投放正确的概率；
（2）为了了解居民生活垃圾分类投放的情况，现随机抽取了小区三类垃圾箱中总共1000吨生活垃圾，数据统计如下（单位：吨）：
| A | B | C | |
| m | 400 | 100 | 100 |
| n | 30 | 240 | 30 |
| p | 20 | 20 | 60 |
12．等腰三角形ABC中，AB=AC=13，BC=10，则底角B的正切值为（ ）
| A． | $\frac{12}{5}$ | B． | $\frac{13}{5}$ | C． | $\frac{5}{12}$ | D． | $\frac{5}{13}$ |
如图，在?ABCD中，AB=6，AD=9，∠BAD的平分线交BC于点E，交DC的延长线于点F，则FC=3．
13．
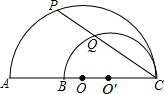如图，AC、BC是两个半圆的直径，∠ACP=30°，若AB=20cm，则PQ的值为（ ）
如图，AC、BC是两个半圆的直径，∠ACP=30°，若AB=20cm，则PQ的值为（ ）| A． | 10cm | B． | 10$\sqrt{3}$cm | C． | 12cm | D． | 16cm |
观察图象，当x＞4时，y＞3？