题目内容
4.若关于x的分式方程$\frac{3}{x-3}$+$\frac{ax}{{x}^{2}-9}$=$\frac{4}{x+3}$无解,求a的值.分析 根据分式方程的解法即可求出a的值.
解答 解:去分母可得:3(x+3)+ax=4(x-3)
∴3x+9+ax=4x-12
∴(a-1)x=-21,
当a-1≠0时,
∵该方程无解,
∴x=$\frac{21}{1-a}$代入x2-9=0
∴$\frac{21}{1-a}$=3或$\frac{21}{1-a}=-3$
解得:a=-6或a=8
当a-1=0时,
此时0=-21,符合题意,
∴a=1,
综上所述,a=1或a=-6或a=8
点评 本题考查分式方程的解法,解题的关键是熟练运用分式方程的解法,本题属于中等题型.

练习册系列答案
相关题目
19.在二元一次方程:2x-3y=5中,用x表示y正确的是( )
| A. | 2x=5+3y | B. | 3y=5-2x | C. | x=$\frac{3y+5}{2}$ | D. | y=$\frac{2x-5}{3}$ |
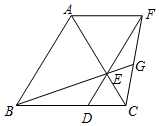 如图,点D,E在等边△ABC的边CB,CA上,且CD=CE,连接DE并延长到点F,使EF=AE,连接AF,CF,BE的延长线交CF于点G.
如图,点D,E在等边△ABC的边CB,CA上,且CD=CE,连接DE并延长到点F,使EF=AE,连接AF,CF,BE的延长线交CF于点G.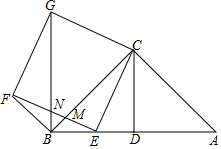 已知△ABC为等腰直角三角形,∠ACB=90°,CD是斜边AB上的中线,且CD=2,点E是线段BD上任意一点,以CE为边向左侧作正方形CEFG,EF交BC于点M,连接BG交EF于点N.
已知△ABC为等腰直角三角形,∠ACB=90°,CD是斜边AB上的中线,且CD=2,点E是线段BD上任意一点,以CE为边向左侧作正方形CEFG,EF交BC于点M,连接BG交EF于点N. 数学活动课上,小明将一直角三角形的纸片沿折痕DE折叠,点A与点B恰好重合,如图所示.若已知AC=8,BC=5,试求出CE长.
数学活动课上,小明将一直角三角形的纸片沿折痕DE折叠,点A与点B恰好重合,如图所示.若已知AC=8,BC=5,试求出CE长.