题目内容
14. 数学活动课上,小明将一直角三角形的纸片沿折痕DE折叠,点A与点B恰好重合,如图所示.若已知AC=8,BC=5,试求出CE长.
数学活动课上,小明将一直角三角形的纸片沿折痕DE折叠,点A与点B恰好重合,如图所示.若已知AC=8,BC=5,试求出CE长.
分析 连接BE,设CE=x,由折叠可知,AE=BE=8-x,把问题转化到Rt△BCE中,使用勾股定理.
解答 解:连接BE,设CE=x ,
,
∵将直角三角形的纸片折叠,A与B重合,折痕为DE,
∴DE是AB的垂直平分线,
∴AE=BE=8-x,
在Rt△BCE中,
BE2=CE2+BC2,
即(8-x)2=x2+52,
解之得x=$\frac{39}{16}$,
即CE=$\frac{39}{16}$.
点评 本题考查图形的翻折变换,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,如本题中折叠前后对应线段相等.

练习册系列答案
相关题目
9.已知a=3b,则代数式$\frac{a+b}{a-b}$的值等于( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
19. 如图,△ABC内接于⊙O,⊙O的半径为5,sin∠B=$\frac{3}{5}$,点D在边AC上,在弧BC上取一点E.使得∠CDE=∠ABC.且AE=$\sqrt{3}$DE.则CD的长为( )
如图,△ABC内接于⊙O,⊙O的半径为5,sin∠B=$\frac{3}{5}$,点D在边AC上,在弧BC上取一点E.使得∠CDE=∠ABC.且AE=$\sqrt{3}$DE.则CD的长为( )
 如图,△ABC内接于⊙O,⊙O的半径为5,sin∠B=$\frac{3}{5}$,点D在边AC上,在弧BC上取一点E.使得∠CDE=∠ABC.且AE=$\sqrt{3}$DE.则CD的长为( )
如图,△ABC内接于⊙O,⊙O的半径为5,sin∠B=$\frac{3}{5}$,点D在边AC上,在弧BC上取一点E.使得∠CDE=∠ABC.且AE=$\sqrt{3}$DE.则CD的长为( )| A. | 2$\sqrt{2}$ | B. | 2 | C. | $\sqrt{3}$ | D. | 2.5 |
3.a表示非负有理数,那么下列说法中正确的是( )
| A. | +a和-(-a)互为相反数 | B. | +a和-a一定不相等 | ||
| C. | -a一定是负数 | D. | -(+a)和+(-a)一定相等 |
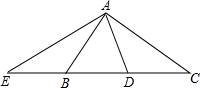 如图,AD是直角三角形ABC斜边上的中线,AE⊥AD交CB延长线于E,则图中一定相似的三角形是C说明理由.
如图,AD是直角三角形ABC斜边上的中线,AE⊥AD交CB延长线于E,则图中一定相似的三角形是C说明理由.