Question

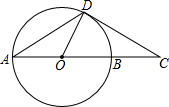如图，点C是⊙O的直径AB延长线上的一点，点D是⊙O上的一点，连接AD，DO，CD，且有∠A=∠C=30°．
（1）求证：CD是⊙O的切线； 
（2）若半径OB=3，求AD的长．

Answer 1

考点：切线的判定,含30度角的直角三角形,勾股定理

专题：

分析：（1）根据等腰三角形性质求出∠ADO=30°，根据三角形内角和定理求出∠ADC=120°，即可求出∠ODC=90°，根据切线的判定推出即可；
（2）连接BD，求出等边三角形DOB，推出BD=3，根据勾股定理求出AD即可．

解答：（1）证明：∵∠A=∠C=30°，
∴∠ADC=120°，
∵AO=OD，
∴∠A=∠ADO=30°，
∴∠ODC=Rt∠，
即OD⊥DC，
∴CD是⊙O的切线；
                  
（2）解：连结DB，
∵∠A=30°，OA=OD，
∴∠ADO=∠A=30°，
∴∠DOB=30°+30°=60°，
∵OD=OB，
∴△DOB是等边三角形，
∴BD=OB=OD=3，
∵AB是⊙O的直径，
∴∠ADB=90°，
∵AB=2OB=6，
∴AD=

AB2-DB2

=

36-9

=3

3

．

点评：本题考查了切线的判定，等腰三角形的性质，勾股定理，含30度角的直角三角形的性质的应用，主要考查学生运用定理进行推理的能力．