题目内容
 如图,AB是半圆O的直径,点P在BA的延长线上,PD切⊙O于点C,BD⊥PD,垂足为D,连接BC、AC.
如图,AB是半圆O的直径,点P在BA的延长线上,PD切⊙O于点C,BD⊥PD,垂足为D,连接BC、AC.(1)求证:△BCD∽△BAC;
(2)若⊙O的半径为3,CD=2
| 2 |
考点:切线的性质,相似三角形的判定与性质
专题:
分析:(1)连接OC,根据切线性质求出∠OCP=90°,推出OC∥BD,求出∠DBC=∠ABC,∠BDC=∠BCA,根据相似三角形的判定推出即可;
(2)根据相似三角形的性质求出BC2=6BD,根据勾股定理得出BC2=BD2+CD2,推出6BD=8+BD2,求出即可.
(2)根据相似三角形的性质求出BC2=6BD,根据勾股定理得出BC2=BD2+CD2,推出6BD=8+BD2,求出即可.
解答:(1)证明: 连结OC,
连结OC,
∵PD切⊙O于点C,
∴OC⊥PD,
∵BD⊥PD,
∴OC∥BD,
∴∠BCO=∠DBC,
∵OC=OB,
∴∠BCO=∠OBC,
∵AB是半圆O的直径,
∴∠ACB=∠CDB=90°,
∴△BCD∽△BAC;
(2)解:∵△BCD∽△BAC,
∴
=
,
∴BC2=6BD,
∵BC2=BD2+CD2,
∴6BD=8+BD2,
解得:BD=4或2(不合题意,舍去),
∴BD=4.
 连结OC,
连结OC,∵PD切⊙O于点C,
∴OC⊥PD,
∵BD⊥PD,
∴OC∥BD,
∴∠BCO=∠DBC,
∵OC=OB,
∴∠BCO=∠OBC,
∵AB是半圆O的直径,
∴∠ACB=∠CDB=90°,
∴△BCD∽△BAC;
(2)解:∵△BCD∽△BAC,
∴
| BD |
| BC |
| BC |
| AB |
∴BC2=6BD,
∵BC2=BD2+CD2,
∴6BD=8+BD2,
解得:BD=4或2(不合题意,舍去),
∴BD=4.
点评:本题考查了切线的性质,相似三角形的性质和判定的应用,主要考查学生运用定理进行推理的能力,题目综合比较强,难度适中.

练习册系列答案
相关题目
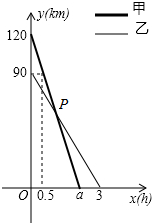 在一条笔直的公路旁依次有A、B、C三个村庄,甲、乙两人同时分别从A、B两村出发,甲骑摩托车,乙骑电动车沿公路匀速驶向C村,最终到达C村.设甲、乙两人到C村的距离y1,y2(km)与行驶时间x(h)之间的函数关系如图所示,请回答下列问题:
在一条笔直的公路旁依次有A、B、C三个村庄,甲、乙两人同时分别从A、B两村出发,甲骑摩托车,乙骑电动车沿公路匀速驶向C村,最终到达C村.设甲、乙两人到C村的距离y1,y2(km)与行驶时间x(h)之间的函数关系如图所示,请回答下列问题: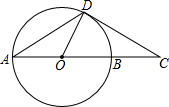 如图,点C是⊙O的直径AB延长线上的一点,点D是⊙O上的一点,连接AD,DO,CD,且有∠A=∠C=30°.
如图,点C是⊙O的直径AB延长线上的一点,点D是⊙O上的一点,连接AD,DO,CD,且有∠A=∠C=30°.