题目内容
已知点C为直径BA的延长线上一点,CD切⊙O于点D,

(Ⅰ)如图①,若∠CDA=26°,求∠DAB的度数;
(Ⅱ)如图②,过点B作⊙O的切线交CD的延长线于点E,若⊙O的半径为3,BC=10,求BE的长.

(Ⅰ)如图①,若∠CDA=26°,求∠DAB的度数;
(Ⅱ)如图②,过点B作⊙O的切线交CD的延长线于点E,若⊙O的半径为3,BC=10,求BE的长.
考点:切线的性质,勾股定理
专题:
分析:(I)根据切线的性质得出∠ODC=90°,求出∠ODA,根据等腰三角形的性质求出即可;
(II)根据切线长定理得出BE=DE,根据勾股定理求出DC,根据勾股定理得出方程,求出方程的解即可.
(II)根据切线长定理得出BE=DE,根据勾股定理求出DC,根据勾股定理得出方程,求出方程的解即可.
解答:解:(I)
如图①,连接OD,
∵CD切⊙O于点D,
∴∠ODC=90°,
∴∠CDA+∠ODA=90°,
∵∠CDA=26°,
∴∠ADO=64°,
∵OD=OA,
∴∠DAB=∠ODA=64°;
(II)如图②,连接OD,
在Rt△ODC中,OC=BC-OB=10-3=7,
CD=
=
=2
,
∵ED、EB分别为⊙O的切线,
∴ED=EB,
在Rt△CBE中,设BE=x,由EC2=EB2+BC2得:(x+2
)2=x2+102,
解得:x=
,
∴BE的长是
.

如图①,连接OD,
∵CD切⊙O于点D,
∴∠ODC=90°,
∴∠CDA+∠ODA=90°,
∵∠CDA=26°,
∴∠ADO=64°,
∵OD=OA,
∴∠DAB=∠ODA=64°;
(II)如图②,连接OD,
在Rt△ODC中,OC=BC-OB=10-3=7,
CD=
| OC2-OD2 |
| 72-32 |
| 10 |
∵ED、EB分别为⊙O的切线,
∴ED=EB,
在Rt△CBE中,设BE=x,由EC2=EB2+BC2得:(x+2
| 10 |
解得:x=
| 3 |
| 2 |
| 10 |
∴BE的长是
| 3 |
| 2 |
| 10 |
点评:本题考查了切线的性质,勾股定理,等腰三角形的应用,题目比较典型,难度适中.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知半径为5的⊙O中,弦AB=5,C是圆弧AB上的任意一点,则∠ACB等于( )
| A、30° |
| B、150° |
| C、30°或150° |
| D、30°或120° |
 如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).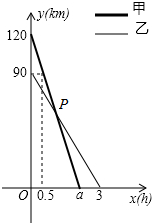 在一条笔直的公路旁依次有A、B、C三个村庄,甲、乙两人同时分别从A、B两村出发,甲骑摩托车,乙骑电动车沿公路匀速驶向C村,最终到达C村.设甲、乙两人到C村的距离y1,y2(km)与行驶时间x(h)之间的函数关系如图所示,请回答下列问题:
在一条笔直的公路旁依次有A、B、C三个村庄,甲、乙两人同时分别从A、B两村出发,甲骑摩托车,乙骑电动车沿公路匀速驶向C村,最终到达C村.设甲、乙两人到C村的距离y1,y2(km)与行驶时间x(h)之间的函数关系如图所示,请回答下列问题: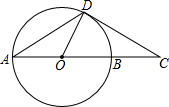 如图,点C是⊙O的直径AB延长线上的一点,点D是⊙O上的一点,连接AD,DO,CD,且有∠A=∠C=30°.
如图,点C是⊙O的直径AB延长线上的一点,点D是⊙O上的一点,连接AD,DO,CD,且有∠A=∠C=30°.