题目内容
现有四张不透明的卡片,它们的背面完全一样,正面分别写有数字-1,2,3,-5,将四张卡片背面朝上,洗匀后放在桌子上.
(1)从中随机抽取一张卡片,正面的数字是奇数的概率为 ;
(2)从中随机抽取一张卡片,把卡片上的数字作为被减数,不放回,再随机抽取一张卡片,把卡片上的数字作为减数,然后计算这两个数的差.请用列表法或树状图的方法,求差大于2的概率.
(1)从中随机抽取一张卡片,正面的数字是奇数的概率为
(2)从中随机抽取一张卡片,把卡片上的数字作为被减数,不放回,再随机抽取一张卡片,把卡片上的数字作为减数,然后计算这两个数的差.请用列表法或树状图的方法,求差大于2的概率.
考点:列表法与树状图法,概率公式
专题:计算题
分析:(1)找出四个数中奇数的个数,即可求出所求的概率;
(2)列表得出所有等可能的情况数,找出差大于2的情况数,即可求出所求的概率.
(2)列表得出所有等可能的情况数,找出差大于2的情况数,即可求出所求的概率.
解答:解:(1)四张卡片中计算为-1,3,-5共三张,
则P=
;
故答案为:
;
(2)列表如下:
所有等可能的情况有12种,其中差大于2的结果有5种,分别为(2,-1);(3,-1);(-1,-5);(2,-5);(3,-5),
则P=
.
则P=
| 3 |
| 4 |
故答案为:
| 3 |
| 4 |
(2)列表如下:
| -1 | 2 | 3 | -5 | |
| -1 | --- | (2,-1) | (3,-1) | (-5,-1) |
| 2 | (-1,2) | --- | (3,2) | (-5,2) |
| 3 | (-1,3) | (2,3) | --- | (-5,3) |
| -5 | (-1,-5) | (2,-5) | (3,-5) | --- |
则P=
| 5 |
| 12 |
点评:此题考查了列表法与树状图法,用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
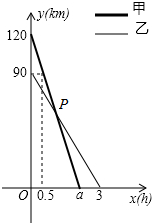 在一条笔直的公路旁依次有A、B、C三个村庄,甲、乙两人同时分别从A、B两村出发,甲骑摩托车,乙骑电动车沿公路匀速驶向C村,最终到达C村.设甲、乙两人到C村的距离y1,y2(km)与行驶时间x(h)之间的函数关系如图所示,请回答下列问题:
在一条笔直的公路旁依次有A、B、C三个村庄,甲、乙两人同时分别从A、B两村出发,甲骑摩托车,乙骑电动车沿公路匀速驶向C村,最终到达C村.设甲、乙两人到C村的距离y1,y2(km)与行驶时间x(h)之间的函数关系如图所示,请回答下列问题: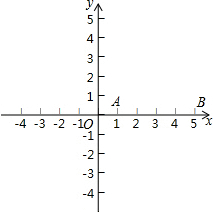 如图,点A与点B的坐标分别是(1,0),(5,0),点P是该直角坐标系内的一个动点.
如图,点A与点B的坐标分别是(1,0),(5,0),点P是该直角坐标系内的一个动点.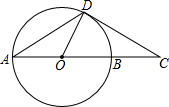 如图,点C是⊙O的直径AB延长线上的一点,点D是⊙O上的一点,连接AD,DO,CD,且有∠A=∠C=30°.
如图,点C是⊙O的直径AB延长线上的一点,点D是⊙O上的一点,连接AD,DO,CD,且有∠A=∠C=30°.