题目内容
已知反比例函数的图象经过点A(3,4),则当-6<x<-3时,y的取值范围是 .
考点:反比例函数的性质
专题:
分析:设反比例函数关系式为y=
(k≠0),利用待定系数法可得反比例函数关系式y=
,根据反比例函数的性质可得在图象的每一支上,y随自变量x的增大而减小,然后求出当x=-6时,y=-2,当x=-3时,y=-4,进而可得答案.
| k |
| x |
| 12 |
| x |
解答:解:设反比例函数关系式为y=
(k≠0),
∵图象经过点A(3,4),
∴k=12,
∴y=
,
当x=-6时,y=-2,
当x=-3时,y=-4,
∴当-6<x<-3时,-4<y<-2,
故答案为:-4<y<-2.
| k |
| x |
∵图象经过点A(3,4),
∴k=12,
∴y=
| 12 |
| x |
当x=-6时,y=-2,
当x=-3时,y=-4,
∴当-6<x<-3时,-4<y<-2,
故答案为:-4<y<-2.
点评:此题主要考查了反比例函数的性质,以及待定系数法求反比例函数解析式,对于反比例函数y=
,当k>0时,在每一个象限内,函数值y随自变量x的增大而减小;当k<0时,在每一个象限内,函数值y随自变量x增大而增大.
| k |
| x |

练习册系列答案
相关题目
 如图,数轴上有A、B、C、D四个点,其中表示互为相反数的点是( )
如图,数轴上有A、B、C、D四个点,其中表示互为相反数的点是( )| A、点A与点D |
| B、点A与点C |
| C、点B与点D |
| D、点B与点C |
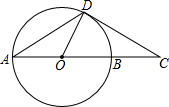 如图,点C是⊙O的直径AB延长线上的一点,点D是⊙O上的一点,连接AD,DO,CD,且有∠A=∠C=30°.
如图,点C是⊙O的直径AB延长线上的一点,点D是⊙O上的一点,连接AD,DO,CD,且有∠A=∠C=30°. 如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形),当四边形ABCD满足
如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形),当四边形ABCD满足