题目内容
15.将分别标有数字1,2,3的三张卡片洗匀后,背面朝上放在桌面上.(1)随机地抽取一张,求P(奇数);
(2)随机地抽取一张作为十位上的数字(不放回),再抽取一张作为个位上的数字,求组成的两位数是4的倍数的概率.
分析 (1)先求出这组数中奇数的个数,再利用概率公式解答即可;
(2)根据题意列举出能组成的数的个数及组成的两位数是4的倍数的个数,再利用概率公式解答.
解答 解:(1)∵随机地抽取一张,所有可能的情况是:1,2,3三种,且它们出现的可能性相等.而结果出现奇数的有1,3两种,
∴P(奇数)=$\frac{2}{3}$;
(2)根据题意画树状图如下:
则组成的两位数有:12、13、21、23、31、32,其中是4的倍数的有12、32,
从而所求概率P=$\frac{2}{6}$=$\frac{1}{3}$.
点评 此题主要考查了树状图法与列表法求概率.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
10.若关于x的一元二次方程kx2-2x-1=0有两个不相等的实数根,则k的取值范围是( )
| A. | k>1 | B. | k>-1且k≠0 | C. | k≥-1且k≠0 | D. | k<1且k≠0 |
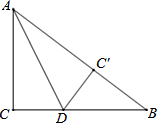 如图,有一块直角三角形ABC纸片,∠ACB=90°,AC=6,BC=8,现将直角边AC沿直线AD折叠,使它落在斜边AB上,点C与点C'重合,求CD的长.
如图,有一块直角三角形ABC纸片,∠ACB=90°,AC=6,BC=8,现将直角边AC沿直线AD折叠,使它落在斜边AB上,点C与点C'重合,求CD的长.