题目内容
4.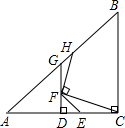 如图,CE=GF,AC=BC,∠ACB=90°,D是中点,DG⊥AC,FH⊥FC.
如图,CE=GF,AC=BC,∠ACB=90°,D是中点,DG⊥AC,FH⊥FC.(1)求证:DG=DC;
(2)判断FH和FC的数量关系.
分析 (1)欲证明DG=CD,因为AD=DC,所以只要证明AD=DG即可.
(2)欲证明FH=FC,只要证明△GFH≌△EFC即可.
解答 (1)证明:∵AC=CB,∠ACB=90°,
∴∠A=∠B=45°,
∵DG⊥AC,
∴∠ADG=90°
∴∠AGD=90°-∠A=45°,
∴∠A=∠AGD,
∴DG=AD,
∵AD=DC,
∴DG=DC.
(2)解:∵DG=DC,FG=EC,
∴DF=DE,
∵∠FDE=90°,
∴∠DFE=∠DEF=45°,
∴∠FEC=180°-∠DEF=135°,
∵∠AGD=45°,
∴∠FGH=180°-∠AGD=135°,
∴∠FEC=∠FGH,
∵FH⊥FC,
∴∠HFC=90°,
∴∠GFH+∠DFC=90°,
∵∠DFC+∠FCD=90°,
∴∠GFH=∠FCE,
在△GFH和△ECF中,
$\left\{\begin{array}{l}{∠FGH=∠FEC}\\{FG=EC}\\{∠GFH=∠ECF}\end{array}\right.$,
∴△GFH≌△ECF,
∴FH=FC.
点评 本题考查全等三角形的判定和性质、等腰直角三角形的性质,解题的关键是证明∠FGH=∠FEC=135°,属于中考常考题型.

练习册系列答案
相关题目
 如图,DE∥BC,EC=AD,AE=2cm,AB=7.5cm,求DB的长.
如图,DE∥BC,EC=AD,AE=2cm,AB=7.5cm,求DB的长. 如图,在平面直角坐标系,点A的坐标为(2,4),点B的坐标为(4,0),直线l到点O、点A、点B的距离比为2:1:1,则直线l的解析式为y=-2x+$\frac{16}{3}$或y=-2x+16或y=6x-16或y=-$\frac{2}{5}$x+$\frac{16}{5}$.
如图,在平面直角坐标系,点A的坐标为(2,4),点B的坐标为(4,0),直线l到点O、点A、点B的距离比为2:1:1,则直线l的解析式为y=-2x+$\frac{16}{3}$或y=-2x+16或y=6x-16或y=-$\frac{2}{5}$x+$\frac{16}{5}$.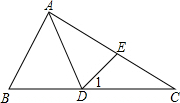 如图,在△ABC中,∠B=2∠C,AD是△ABC的角平分线,∠1=∠C,求证:AC=AB+BD.
如图,在△ABC中,∠B=2∠C,AD是△ABC的角平分线,∠1=∠C,求证:AC=AB+BD.