题目内容
8.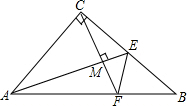 如图,△ABC中,AC=BC,∠ACB=90°.若AE为△ABC的中线,CF⊥AE,垂足为M,交AB于F点,求证:
如图,△ABC中,AC=BC,∠ACB=90°.若AE为△ABC的中线,CF⊥AE,垂足为M,交AB于F点,求证:(1)AE-EF=CF;
(2)AF=2BF.
分析 (1)作BN⊥BC交CF的延长线于N,先证明△ACE≌△CBN得EC=BN=EB,再证明△BFE≌△BFN得EF=FN,根据线段和差定义即可解决.
(2)由AC∥BN得$\frac{AF}{BF}=\frac{AC}{BC}$=2,即可证明.
解答 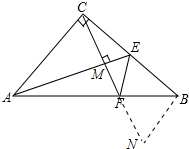 (1)证明:作BN⊥BC交CF的延长线于N.
(1)证明:作BN⊥BC交CF的延长线于N.
∵∠ACB=∠CBN=90°,
∴∠CAE+∠ACM=90°,∠ACM+∠NCB=90°,
∴∠CAE=∠NCB,
在△ACE和△CBN中,
$\left\{\begin{array}{l}{∠CAE=∠BCN}\\{AC=BC}\\{∠ACE=∠CBN}\end{array}\right.$,
∴△ACE≌△CBN,
∴CE=BN=EB,AE=CN,
∵CA=CB,∠ACB=90°,
∴∠ABC=45°,∵∠CBN=90°,
∴∠CBA=∠ABN=45°
在△FBE和△FBN中,
$\left\{\begin{array}{l}{EB=BN}\\{∠EBF=∠NBF}\\{BF=BF}\end{array}\right.$,
∴△BFE≌△BFN,
∴EF=FN,
∴AE-EF=CN-FN=CF.
(2)由(1)可知BN=EC=EB,
∵AC=BC,
∴AC=2BN,
∵∠ACB+∠CBN=180°,
∴AC∥BN,
∴$\frac{AF}{BF}=\frac{AC}{BC}$=2,
∴AF=2BF.
点评 本题考查全等三角形的判定和性质、等腰直角三角形的性质、平行线分线段成比例定理等知识,添加辅助线构造全等三角形是解决问题的关键,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.下列说法正确的是( )
| A. | 直线AB和直线BA是两条直线 | B. | 射线AB和射线BA是两条射线 | ||
| C. | 线段AB和线段BA是两条线段 | D. | 直线和射线可以度量 |
17.$\sqrt{4}$的平方根等于( )
| A. | 2 | B. | -2 | C. | ±2 | D. | ±$\sqrt{2}$ |
 如图,抛物线$y=-\frac{1}{2}{x^2}+4x-6$与x轴相交于点A、B,与y轴相交于点C,抛物线对称轴与x轴相交于点M,
如图,抛物线$y=-\frac{1}{2}{x^2}+4x-6$与x轴相交于点A、B,与y轴相交于点C,抛物线对称轴与x轴相交于点M, 如图,在平面直角坐标系,点A的坐标为(2,4),点B的坐标为(4,0),直线l到点O、点A、点B的距离比为2:1:1,则直线l的解析式为y=-2x+$\frac{16}{3}$或y=-2x+16或y=6x-16或y=-$\frac{2}{5}$x+$\frac{16}{5}$.
如图,在平面直角坐标系,点A的坐标为(2,4),点B的坐标为(4,0),直线l到点O、点A、点B的距离比为2:1:1,则直线l的解析式为y=-2x+$\frac{16}{3}$或y=-2x+16或y=6x-16或y=-$\frac{2}{5}$x+$\frac{16}{5}$.
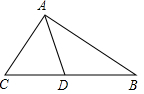 如图,△ABC中,∠C=2∠B,AD是△ABC的角平分线,求证:AB=AC+CD.
如图,△ABC中,∠C=2∠B,AD是△ABC的角平分线,求证:AB=AC+CD.
 如图,AB∥CD,∠CDE=121°,GF交∠DEB的平分线EF于点F,∠AGF=140°,求∠F的度数.
如图,AB∥CD,∠CDE=121°,GF交∠DEB的平分线EF于点F,∠AGF=140°,求∠F的度数.