题目内容
10.在△ABC中,AB=AC,若其周长为20,则AB边的取值范围是( )| A. | 1<AB<4 | B. | 5<AB<10 | C. | 4<AB<8 | D. | 4<AB<10 |
分析 设AB=AC=x,由三角形的三边关系定理得出x>5,再由边长为正数得出x<10,即可得出结果.
解答 解:设AB=AC=x,
则BC=20-2x,
由三角形的三边关系得:x+x>20-2x,
解得:x>5,
又∵20-2x>0,
解得:x<10,
∴5<x<10,
即5<AB<10;
故选:B.
点评 本题考查了三角形的三边关系、等腰三角形的性质;熟练掌握三角形的三边关系定理是解决问题的关键.

练习册系列答案
相关题目
1.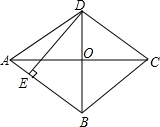 如图,菱形ABCD的两条对角线相交于点O,若AC=8,BD=6,过点D作DE⊥AB,垂足为E,则DE的长是( )
如图,菱形ABCD的两条对角线相交于点O,若AC=8,BD=6,过点D作DE⊥AB,垂足为E,则DE的长是( )
 如图,菱形ABCD的两条对角线相交于点O,若AC=8,BD=6,过点D作DE⊥AB,垂足为E,则DE的长是( )
如图,菱形ABCD的两条对角线相交于点O,若AC=8,BD=6,过点D作DE⊥AB,垂足为E,则DE的长是( )| A. | 2.4 | B. | 4.8 | C. | 7.2 | D. | 10 |
18. 如图,在3×3的正方形网格中,每个小正方形的边长都相等,阴影部分的图案是由3个小正方形组成的,我们称这一的图案为I.形,在网格中通过平移还能画出不同位置的I.形图案的个数是( )
如图,在3×3的正方形网格中,每个小正方形的边长都相等,阴影部分的图案是由3个小正方形组成的,我们称这一的图案为I.形,在网格中通过平移还能画出不同位置的I.形图案的个数是( )
 如图,在3×3的正方形网格中,每个小正方形的边长都相等,阴影部分的图案是由3个小正方形组成的,我们称这一的图案为I.形,在网格中通过平移还能画出不同位置的I.形图案的个数是( )
如图,在3×3的正方形网格中,每个小正方形的边长都相等,阴影部分的图案是由3个小正方形组成的,我们称这一的图案为I.形,在网格中通过平移还能画出不同位置的I.形图案的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
2.若m>-1,则下列各式中错误的是( )
| A. | 6m>-6 | B. | m+1>0 | C. | -5m<-5 | D. | 1-m<2 |
 如图,∠A=65°,∠B=75°,将纸片的一角折叠,使点C落在△ABC内,若∠2=20°,则∠1=60°度.
如图,∠A=65°,∠B=75°,将纸片的一角折叠,使点C落在△ABC内,若∠2=20°,则∠1=60°度. 如图,点P是直线l外一点,PO⊥l,垂足为O点,则点P到直线l的距离是线段PO的长度.
如图,点P是直线l外一点,PO⊥l,垂足为O点,则点P到直线l的距离是线段PO的长度.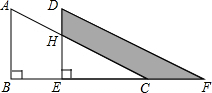 如图,将△ABC沿BC方向平移得到△DEF,若∠B=90°,AB=6,BC=8,BE=2,DH=1.5,阴影部分的面积为10.5.
如图,将△ABC沿BC方向平移得到△DEF,若∠B=90°,AB=6,BC=8,BE=2,DH=1.5,阴影部分的面积为10.5. 如图,在边长为1的正方形网格中,平移△ABC,使点A平移到点D.
如图,在边长为1的正方形网格中,平移△ABC,使点A平移到点D.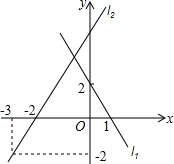 如图,直线l1、l2相交于点A,试求出点A的坐标.
如图,直线l1、l2相交于点A,试求出点A的坐标.