题目内容
1.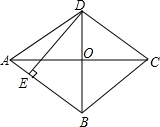 如图,菱形ABCD的两条对角线相交于点O,若AC=8,BD=6,过点D作DE⊥AB,垂足为E,则DE的长是( )
如图,菱形ABCD的两条对角线相交于点O,若AC=8,BD=6,过点D作DE⊥AB,垂足为E,则DE的长是( )| A. | 2.4 | B. | 4.8 | C. | 7.2 | D. | 10 |
分析 根据“菱形的面积等于对角线乘积的一半”可以求得该菱形的面积.菱形的面积还等于底乘以高,所以可得DE的长度.
解答 解:∵四边形ABCD是菱形,AC=8,BD=6,
∴AC⊥OD,AO=$\frac{1}{2}$AC=4,BO=$\frac{1}{2}$BD=3,
∴由勾股定理得到:AB=$\sqrt{A{O}^{2}+B{O}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5.
又∵$\frac{1}{2}$AC•BD=AB•DE.
∴DE=$\frac{AC•BD}{2AB}$=4.8.
故选:B.
点评 本题考查了菱形的性质.属于中等难度的题目,解答本题关键是掌握①菱形的对角线互相垂直且平分,②菱形的面积等于底乘以底边上的高,还等于对角线乘积的一半.

练习册系列答案
相关题目
10.在△ABC中,AB=AC,若其周长为20,则AB边的取值范围是( )
| A. | 1<AB<4 | B. | 5<AB<10 | C. | 4<AB<8 | D. | 4<AB<10 |
 如果AB∥CF,DE∥CF,∠DCB=40°,∠D=30°,求∠B的度数.
如果AB∥CF,DE∥CF,∠DCB=40°,∠D=30°,求∠B的度数.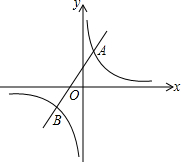 如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=ax+b的图象交于点A(1,4),点B(m,-2)
如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=ax+b的图象交于点A(1,4),点B(m,-2)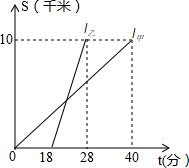 某中学甲、乙两位教师先后从学校出发,到距学校10km的培训中心参加新教材培训学习,图中I甲,I乙分别表示甲、乙两位教师从学校到培训中心所走的路程S(km)随时间t(分钟)变化的函数图象.
某中学甲、乙两位教师先后从学校出发,到距学校10km的培训中心参加新教材培训学习,图中I甲,I乙分别表示甲、乙两位教师从学校到培训中心所走的路程S(km)随时间t(分钟)变化的函数图象.