题目内容
20. 如图,∠A=65°,∠B=75°,将纸片的一角折叠,使点C落在△ABC内,若∠2=20°,则∠1=60°度.
如图,∠A=65°,∠B=75°,将纸片的一角折叠,使点C落在△ABC内,若∠2=20°,则∠1=60°度.
分析 由∠A、∠B的度数,可求∠C的大小,进而在△CDE中,得出∠CDE与∠CED的和,再在四边形ABED中,即可求解∠1的大小.
解答  解:∵∠A=65°,∠B=75°,则∠C=40°,
解:∵∠A=65°,∠B=75°,则∠C=40°,
在△CDE中,则∠CDE+∠CED=140°,
在四边形ABED中,∠A+∠B+∠ADE+∠BED=360°,
即∠A+∠B+∠CDE+∠1+∠2+∠CED=360°,
65°+75°+140°+20°+∠1=360°,
∠1=60°.
故答案为:60°.
点评 本题考查的是三角形内角和定理、四边形内角和定理和翻折变换的性质,掌握三角形内角和等于180°是解题的关键.

练习册系列答案
相关题目
8.使分式$\frac{2}{2x-6}$有意义的x的取值范围是( )
| A. | x≤3 | B. | x≥3 | C. | x≠3 | D. | x=3 |
10.在△ABC中,AB=AC,若其周长为20,则AB边的取值范围是( )
| A. | 1<AB<4 | B. | 5<AB<10 | C. | 4<AB<8 | D. | 4<AB<10 |
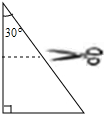 如图所示,是一张直角三角形纸片,其中有一个内角为30°,最小边长为2,点D、E分别是一条直角边和斜边的中点,先将纸片沿DE剪开,然后再将两部分拼成一个四边形,则所得四边形的周长是8或4+2$\sqrt{3}$.
如图所示,是一张直角三角形纸片,其中有一个内角为30°,最小边长为2,点D、E分别是一条直角边和斜边的中点,先将纸片沿DE剪开,然后再将两部分拼成一个四边形,则所得四边形的周长是8或4+2$\sqrt{3}$. 如果AB∥CF,DE∥CF,∠DCB=40°,∠D=30°,求∠B的度数.
如果AB∥CF,DE∥CF,∠DCB=40°,∠D=30°,求∠B的度数.