题目内容
20.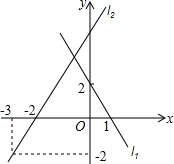 如图,直线l1、l2相交于点A,试求出点A的坐标.
如图,直线l1、l2相交于点A,试求出点A的坐标.
分析 根据待定系数法解出两个直线的解析式后列出方程解答即可.
解答 解:设直线l1的解析式为y=ax+b,
把(1,0)(0,2)代入可得:$\left\{\begin{array}{l}{a+b=0}\\{b=2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-2}\\{b=2}\end{array}\right.$,
解析式为:y=-2x+2;
设直线l2的解析式为y=kx+c,
把(-3,-2)(-2,0)代入可得:$\left\{\begin{array}{l}{-3k+c=-2}\\{-2k+c=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=2}\\{c=4}\end{array}\right.$,
解析式为:y=2x+4,
因为两直线相交可得:2x+4=-2x+2,
解得:x=-0.5,
把x=-0.5代入y=-2x+2=3,
所以点A的坐标为(-0.5,3).
点评 此题考查两直线相交问题,关键是根据待定系数法解出两直线的解析式列出方程.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
10.在△ABC中,AB=AC,若其周长为20,则AB边的取值范围是( )
| A. | 1<AB<4 | B. | 5<AB<10 | C. | 4<AB<8 | D. | 4<AB<10 |
15.已知a-b=1,则a2-b2-2b的值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
5.若二次函数y1=a1x2-1与二次函数y2=a2x2+3图象的形状完全相同,则a1与a2的关系为( )
| A. | a1=a2 | B. | a1=-a2 | C. | a1=±a2 | D. | 无法判断 |
9.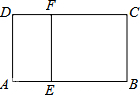 如图,矩形ABCD∽矩形ADFE,AE=1,AB=4,则AD=( )
如图,矩形ABCD∽矩形ADFE,AE=1,AB=4,则AD=( )
 如图,矩形ABCD∽矩形ADFE,AE=1,AB=4,则AD=( )
如图,矩形ABCD∽矩形ADFE,AE=1,AB=4,则AD=( )| A. | 2 | B. | 2.4 | C. | 2.5 | D. | 3 |
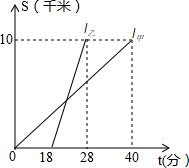 某中学甲、乙两位教师先后从学校出发,到距学校10km的培训中心参加新教材培训学习,图中I甲,I乙分别表示甲、乙两位教师从学校到培训中心所走的路程S(km)随时间t(分钟)变化的函数图象.
某中学甲、乙两位教师先后从学校出发,到距学校10km的培训中心参加新教材培训学习,图中I甲,I乙分别表示甲、乙两位教师从学校到培训中心所走的路程S(km)随时间t(分钟)变化的函数图象.