题目内容
 如图,△ABC的三条角平分线交于点P,已知∠ABC=60°,则∠APC=
如图,△ABC的三条角平分线交于点P,已知∠ABC=60°,则∠APC=考点:三角形内角和定理
专题:计算题
分析:先根据角平分线定义得到∠1=
∠BAC,∠2=
∠ACB,再根据三角形内角和定理得∠APC=180°-∠1-∠2,∠BAC+∠ACB=180°-∠ABC,则∠APC=180°-
(∠BAC+∠ACB)=∠APB=180°-
(180°-∠ABC)=90°+
∠ABC,然后把∠ABC=60°代入计算即可.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解: ∵△ABC的三条角平分线交于点P,
∵△ABC的三条角平分线交于点P,
∴∠1=
∠BAC,∠2=
∠ACB,
∵∠APC=180°-∠1-∠2,
∴∠APC=180°-
(∠BAC+∠ACB),
∵∠BAC+∠ACB=180°-∠ABC,
∴∠APC=180°-
(180°-∠ABC)
=90°+
∠ABC
=90°+
×60°
=120°.
故答案为120°.
 ∵△ABC的三条角平分线交于点P,
∵△ABC的三条角平分线交于点P,∴∠1=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠APC=180°-∠1-∠2,
∴∠APC=180°-
| 1 |
| 2 |
∵∠BAC+∠ACB=180°-∠ABC,
∴∠APC=180°-
| 1 |
| 2 |
=90°+
| 1 |
| 2 |
=90°+
| 1 |
| 2 |
=120°.
故答案为120°.
点评:本题考查了三角形内角和定理:三角形内角和是180°.也考查了角平分线定义和角的计算.关键得出∠APC与∠ABC的数量关系.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
 如图,在Rt△ABC中,∠ACB=90°,∠A=30°,CD是斜边AB上的中线,则图中与CD的长度相等的线段有( )
如图,在Rt△ABC中,∠ACB=90°,∠A=30°,CD是斜边AB上的中线,则图中与CD的长度相等的线段有( )| A、AD与BD |
| B、BD与BC |
| C、AD与BC |
| D、AD、BD与BC |
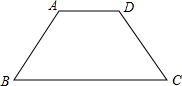 如图,在等腰梯形ABCD中,AD∥BC,∠C=60°,AD=6,AB=8,则BC=( )
如图,在等腰梯形ABCD中,AD∥BC,∠C=60°,AD=6,AB=8,则BC=( )| A、10 | B、12 | C、14 | D、16 |
 娜娜同学发现爸爸西服的袖口上订了一排如图的纽扣,则图中任意的两圆间不存在的位置关系是( )
娜娜同学发现爸爸西服的袖口上订了一排如图的纽扣,则图中任意的两圆间不存在的位置关系是( )| A、外离 | B、内含 | C、外切 | D、内切 |
 已知,如图,在平面直角坐标系内,点A的坐标为(0,12),经过原点的直线l,与经过点A的直线12相交于点B,点B的坐标为(9,3).
已知,如图,在平面直角坐标系内,点A的坐标为(0,12),经过原点的直线l,与经过点A的直线12相交于点B,点B的坐标为(9,3). 在如图所示的直角坐标系中,解答下列问题:
在如图所示的直角坐标系中,解答下列问题: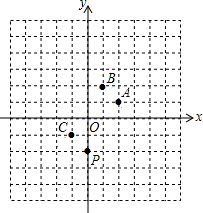 如图,在平面直角坐标系中,动点P从(0,-2)位置开始,一次关于点A、B、C作循环对称的跳动,即第一次跳到点P关于点A对称点M处,第二次接着跳到点M关于点B的对称点N处,第三次跳到点N关于点C的对称点处,…,按如此方法继续跳下去,则经过第2015次跳动之后,动点P落点处的坐标为
如图,在平面直角坐标系中,动点P从(0,-2)位置开始,一次关于点A、B、C作循环对称的跳动,即第一次跳到点P关于点A对称点M处,第二次接着跳到点M关于点B的对称点N处,第三次跳到点N关于点C的对称点处,…,按如此方法继续跳下去,则经过第2015次跳动之后,动点P落点处的坐标为 如图,已知AB是⊙O的直径,点C在⊙O上,点D是BC的中点,若AC=10cm,则OD=
如图,已知AB是⊙O的直径,点C在⊙O上,点D是BC的中点,若AC=10cm,则OD=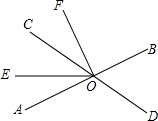 如图,直线AB和CD相交于点O,OE把∠AOC分成两部分且∠AOE:∠EOC=3:5,OF平分∠BOE.
如图,直线AB和CD相交于点O,OE把∠AOC分成两部分且∠AOE:∠EOC=3:5,OF平分∠BOE.