题目内容
12.已知:⊙O1和⊙O2的直径分别为5cm和3cm,两圆的圆心距是9cm,则两圆的位置关系是( )| A. | 外离 | B. | 外切 | C. | 相交 | D. | 内切 |
分析 根据两圆的半径之和小于两圆的圆心距时,两圆外离解答即可.
解答 解:∵⊙O1和⊙O2的直径分别为5cm和3cm,
∴⊙O1和⊙O2的半径分别为2.5cm和1.5cm,
∵2.5+1.5<9,
∴两圆外离,
故选:A.
点评 本题考查了由数量关系来判断两圆位置关系,当P表示圆心距,R,r分别表示两圆的半径,两圆外离,则P>R+r;两圆外切,则P=R+r;两圆相交,则R-r<P<R+r;两圆内切,则P=R-r;两圆内含,则P<R-r.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
20. 某区对参加2014年中考的5000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图的一部分.
某区对参加2014年中考的5000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图的一部分.
请根据图表信息回答下列问题:
(1)本次调查的样本容量为200;在频数分布表中,a的值为60,b的值为0.05,并将频数分布直方图补充完整;
(2)若视力在4.9以上(含4.9)均属正常,则视力正常的人数占被统计人数的百分比是35%;
(3)根据上述信息估计全区初中毕业生中视力正常的学生有多少人?
 某区对参加2014年中考的5000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图的一部分.
某区对参加2014年中考的5000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图的一部分.请根据图表信息回答下列问题:
| 视力 | 频数(人) | 频率 |
| 4.0≤x<4.3 | 20 | 0.1 |
| 4.3≤x<4.6 | 40 | 0.2 |
| 4.6≤x<4.9 | 70 | 0.35 |
| 4.9≤x<5.2 | a | 0.3 |
| 5.2≤x<5.5 | 10 | b |
(2)若视力在4.9以上(含4.9)均属正常,则视力正常的人数占被统计人数的百分比是35%;
(3)根据上述信息估计全区初中毕业生中视力正常的学生有多少人?
2.如果两个相似三角形对应高的比为3:5,面积之比为2:x,那么x的算术平方根为( )
| A. | $\frac{5\sqrt{2}}{3}$ | B. | $±\frac{5\sqrt{2}}{3}$ | C. | $\frac{50}{9}$ | D. | $±\frac{50}{9}$ |
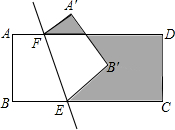 如图,矩形ABCD中,AB=2cm,BC=5cm,将四边形ABEF沿直线EF折叠,点A落在A′处,点B落在B′处,则阴影部分的周长为14cm.
如图,矩形ABCD中,AB=2cm,BC=5cm,将四边形ABEF沿直线EF折叠,点A落在A′处,点B落在B′处,则阴影部分的周长为14cm. 六一儿童节期间,某眼镜店开展优惠配镜活动,某款式的眼镜广告如图:请你为广告补上原价.
六一儿童节期间,某眼镜店开展优惠配镜活动,某款式的眼镜广告如图:请你为广告补上原价. 如图,点A是反比例函数y=$\frac{3}{x}$图象上一点,AD⊥y轴于D交y=$\frac{1}{x}$的图象于点B,AE⊥x轴于E交y=$\frac{1}{x}$的图象于点C,则四边形OBAC(阴影部分)的面积为( )
如图,点A是反比例函数y=$\frac{3}{x}$图象上一点,AD⊥y轴于D交y=$\frac{1}{x}$的图象于点B,AE⊥x轴于E交y=$\frac{1}{x}$的图象于点C,则四边形OBAC(阴影部分)的面积为( )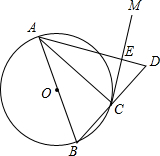 如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线CM.
如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线CM.