题目内容
1.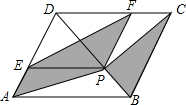 如图,菱形ABCD的边长为2,较短的对角线BD的长为3,P是BD上一点,PE∥AB,PF∥AD,分别交菱形两边于点E、F,则图中阴影部分面积为$\frac{9}{4}$$\sqrt{3}$.
如图,菱形ABCD的边长为2,较短的对角线BD的长为3,P是BD上一点,PE∥AB,PF∥AD,分别交菱形两边于点E、F,则图中阴影部分面积为$\frac{9}{4}$$\sqrt{3}$.
分析 先判断四边形DEPF是菱形,得出△DOE和△POF的面积相等,根据菱形的对称性求出△ABP和△CBP的面积相等,再根据菱形的对称性判断出阴影部分的面积等于菱形ABCD面积的一半,然后根据菱形的面积等于对角线乘积的一半列式进行计算即可得解.
解答 解:如图,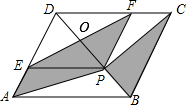
在菱形ABCD中,
∵PE∥AB,PF∥AD,
∴四边形DEPF是菱形,
∴S△DOE=S△FOP,
∵菱形是轴对称图形,
∴△ABP和△CBP面积相等,
∵菱形的对角线把菱形分成四个全等的三角形,
∴阴影部分的面积等于菱形面积的一半,
∵AB=2,BD=3,
∴AC=2$\sqrt{{2}^{2}-1.{5}^{2}}$=3$\sqrt{3}$
∴菱形的面积=$\frac{1}{2}$×3×3$\sqrt{3}$=$\frac{9}{2}$$\sqrt{3}$,
∴阴影部分的面积为$\frac{1}{2}$×$\frac{9}{2}$$\sqrt{3}$=$\frac{9}{4}$$\sqrt{3}$.
故答案为:$\frac{9}{4}$$\sqrt{3}$.
点评 本题考查了菱形的对称性,菱形的面积等于对角线乘积的一半,判断出阴影部分的面积等于菱形ABCD面积的一半是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.|-$\frac{1}{2015}$|的相反数是( )
| A. | 2015 | B. | -2015 | C. | $\frac{1}{2015}$ | D. | -$\frac{1}{2015}$ |
12.可以来证明命题“若a2<0.04,则a<0.2”是假命题的反例( )
| A. | 可以是a=-0.2,不可以是a=-2 | |
| B. | 可以是a=-2,不可以是a=-0.2 | |
| C. | 可以是a=-0.2,也可以是a=-2 | |
| D. | 既不可以是a=-0.2,也不可以是a=-2 |
9.下列计算正确的是( )
| A. | $\sqrt{5}-\sqrt{3}=\sqrt{2}$ | B. | $\sqrt{6}÷2=\sqrt{3}$ | C. | $\sqrt{2}$•$\sqrt{3}=\sqrt{6}$ | D. | $\sqrt{8}=4\sqrt{2}$ |
6.在四边形ABCD中,若∠A:∠B:∠C:∠D=5:m:4:n,则( )
| A. | m+n=9 | B. | 4m=5n | C. | 5m=4n | D. | 以上都不对 |
 如图,在?ABCD中,∠ABC的平分线交AD于点E,∠C=110°,BC=4cm,CD=3cm,则∠BED=145°,DE=1cm.
如图,在?ABCD中,∠ABC的平分线交AD于点E,∠C=110°,BC=4cm,CD=3cm,则∠BED=145°,DE=1cm. 如图所示,若四条直线两两相交于不同点,则图中有12对对顶角,有48对同位角,有24对内错角,有24对同旁内角.
如图所示,若四条直线两两相交于不同点,则图中有12对对顶角,有48对同位角,有24对内错角,有24对同旁内角. 如图所示,点A在点O的北偏东50°方向,点B在点O的南偏东10°方向上,则∠AOB=120°.
如图所示,点A在点O的北偏东50°方向,点B在点O的南偏东10°方向上,则∠AOB=120°.