题目内容
4. 如图,△ABC和△EFD的边BC和FD在同一条直线上,顶点A,E在BF两侧,其中∠B=∠F,BD=FC.要使△ABC≌△EFD,则需要添加的一个条件时AB=EF 或∠ACB=∠EDF或AC∥DE或∠A=∠E.(只写一种即可)
如图,△ABC和△EFD的边BC和FD在同一条直线上,顶点A,E在BF两侧,其中∠B=∠F,BD=FC.要使△ABC≌△EFD,则需要添加的一个条件时AB=EF 或∠ACB=∠EDF或AC∥DE或∠A=∠E.(只写一种即可)
分析 通过已知可以得到三角形中有一边一角对应相等,根据SAS或ASA或AAS即可写出添加的条件.
解答 解:∵BD=FC,
∴BC=FD.
在△ABC和△EFD中,已知BC=FD,∠B=∠F,根据SAS可以得到可以添加的条件是:AB=EF;
依据ASA可以添加∠ACB=∠EDF或AC∥DE;
依据AAS可以添加∠A=∠E.
故答案是:AB=EF 或∠ACB=∠EDF或AC∥DE或∠A=∠E.
点评 本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS,正确掌握定理是关键.

练习册系列答案
 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
15.给出下列计算:①(m-n)(-m-n)=-m2-n2;②(-2s+t)2=4s2-4st+t2;③$\frac{x+y}{x-y}$÷(x2-y2)=(x+y)2.其中正确的是( )
| A. | ①②③ | B. | ②③ | C. | ② | D. | ③ |
12.解不等式组$\left\{\begin{array}{l}{x+3(2-x)≤8}\\{\frac{1+2x}{3}>x-1}\end{array}\right.$,并将其解集在数轴上表示出来.
19. 如图,在Rt△ABC中,∠C=90°,BD是△ABC的角平分线,过点D作DE⊥AB,垂足为E,则下列结论错误的是( )
如图,在Rt△ABC中,∠C=90°,BD是△ABC的角平分线,过点D作DE⊥AB,垂足为E,则下列结论错误的是( )
 如图,在Rt△ABC中,∠C=90°,BD是△ABC的角平分线,过点D作DE⊥AB,垂足为E,则下列结论错误的是( )
如图,在Rt△ABC中,∠C=90°,BD是△ABC的角平分线,过点D作DE⊥AB,垂足为E,则下列结论错误的是( )| A. | DE=DC | B. | ∠ADE=∠ABC | C. | BE=BC | D. | ∠ADE=∠ABD |
16.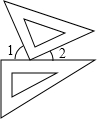 一副三角板按如图方式摆放,且∠1的度数比∠2的度数大50°,若设∠1=x°∠2=y°,则可得到方程组为( )
一副三角板按如图方式摆放,且∠1的度数比∠2的度数大50°,若设∠1=x°∠2=y°,则可得到方程组为( )
 一副三角板按如图方式摆放,且∠1的度数比∠2的度数大50°,若设∠1=x°∠2=y°,则可得到方程组为( )
一副三角板按如图方式摆放,且∠1的度数比∠2的度数大50°,若设∠1=x°∠2=y°,则可得到方程组为( )| A. | $\left\{\begin{array}{l}{x=y+50}\\{x+y=90}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=y-50}\\{x+y=90}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=y-50}\\{x+y=180}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=y+50}\\{x+y=180}\end{array}\right.$ |
13. 如图,B、C是⊙A上的两点,AB的垂直平分线与⊙A交于E、F两点,与线段AC交于D点.若∠BFC=20°,则∠DBC=( )
如图,B、C是⊙A上的两点,AB的垂直平分线与⊙A交于E、F两点,与线段AC交于D点.若∠BFC=20°,则∠DBC=( )
 如图,B、C是⊙A上的两点,AB的垂直平分线与⊙A交于E、F两点,与线段AC交于D点.若∠BFC=20°,则∠DBC=( )
如图,B、C是⊙A上的两点,AB的垂直平分线与⊙A交于E、F两点,与线段AC交于D点.若∠BFC=20°,则∠DBC=( )| A. | 30° | B. | 29° | C. | 28° | D. | 20° |
1.m16可以写成( )
| A. | m8+m8 | B. | m8•m8 | C. | m2•m8 | D. | m4•m4 |