题目内容
15．化简：（1）$\frac{b}{a-b}$+$\frac{{b}^{3}}{{a}^{3}-2{a}^{2}b+a{b}^{2}}$÷$\frac{ab+{b}^{2}}{{b}^{2}-{a}^{2}}$．
（2）$\frac{3-x}{2x-4}$÷（x+2-$\frac{5}{x-2}$）．
分析 （1）原式先计算除法运算，再计算加减运算即可得到结果；
（2）原式括号中两项通分并利用同分母分式的减法法则计算，同时利用除法法则计算，约分即可得到结果．
解答 解：（1）原式=$\frac{a}{a-b}$-$\frac{{b}^{3}}{a（a-b）^{2}}$•$\frac{（a+b）（a-b）}{b（a+b）}$=$\frac{b}{a-b}$-$\frac{{b}^{2}}{a（a-b）}$=$\frac{b（a-b）}{a（a-b）}$=$\frac{b}{a}$；
（2）原式=-$\frac{x-3}{2（x-2）}$•$\frac{x-2}{（x+3）（x-3）}$=-$\frac{1}{2（x+3）}$．
点评 此题考查了实数的运算，熟练掌握运算法则是解本题的关键．
练习册系列答案
名师指导期末冲刺卷系列答案
相关题目
数轴上点A、B的位置如图所示，则A，B间的距离是7．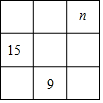
我们知道，在三阶幻方中每行、每列、毎条对角线上的三个数之和都是相等的，在如图的三阶幻方中已经填入了两个数9和15，则图中最右上角的数n应该是12．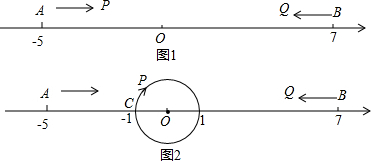
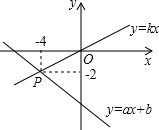10．若方程（m-3）x${\;}^{{m}^{2}-7}$-x+3=0是关于x的一元二次方程，则方程（ ）
| A． | 无实数根 | B． | 有两个相等的实数根 | ||
| C． | 有两个不相等的实数根 | D． | 有一个根 |
如图所示，已知函数y=ax+b和y=kx的图象相交于点P，则根据图象可得关于x，y的二元一次方程组$\left\{\begin{array}{l}y=ax+b\\ y=kx\end{array}$的解是$\left\{\begin{array}{l}{x=-4}\\{y=-2}\end{array}\right.$．
