题目内容
3．甲、乙两人从学校到2000米远的展览馆去参观，甲走了4分钟后乙才出发，已知甲的速度是80米/分，乙的速度是100米/分．（1）乙出发后经过多长时间能追上甲？
（2）乙追上甲时离展览馆还有多远？
分析 （1）根据甲乙两人所走的路程相等，设乙要x分钟才能追上甲，列方程求解；
（2）乙追上甲时离展览馆的距离=1000-乙所走的路程．
解答 解：（1）设乙要x分钟才能追上甲，
根据题意得：100x=80x+4×80，
解方程得：x=16．
答：乙出发后经过16分钟能追上甲；
（2）乙追上甲时离展览馆还有=2000-100×16=400（米）
答：追上甲时离展览馆还有400米．
点评 本题考查了一元一次方程的应用，它属于追及问题中的简单题型，关键是运用“两人所走的路程相等”这一相等关系，列出方程求解．
练习册系列答案
相关题目
如图，多边形的相邻两边均互相垂直，则这个多边形的周长为2a+2b．
14．
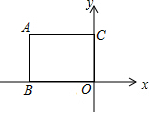如图，以长方形OCAB的顶点O为原点建立直角坐标系，点B、C分别在x、y轴上，若OB=5，OC=3，则点A可以表示为（ ）
如图，以长方形OCAB的顶点O为原点建立直角坐标系，点B、C分别在x、y轴上，若OB=5，OC=3，则点A可以表示为（ ）| A． | （-5，3） | B． | （5，-3） | C． | （-3，5） | D． | （3，-5） |
11．在平面直角坐标系内有一点A的坐标是（-3，5），则点A到y轴的距离是（ ）
| A． | 3 | B． | 5 | C． | -3 | D． | -5 |
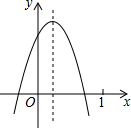二次函数y=ax2+bx+c（a≠0）的图象如图，则下列结论：①ac＜0；②方程ax2+bx+c=0的两根之和大于0；③y随x的增大而增大；④a-b+c＜0．其中正确的是（ ）
如图，矩形ABCD的对角线AC、BD交于点O，CE∥BD，DE∥AC．
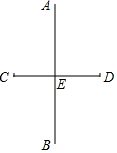如图，直线AB是线段CD的垂直平分线，则下列结论正确的有（ ）