题目内容
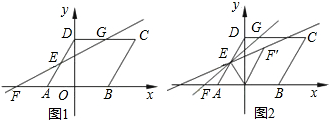
16．
如图，BD⊥AC于D，EF⊥AC于F，MD∥BC，∠1=∠2．求证：（1）BD∥EF；
（2）∠AMD=∠AGF．
分析 （1）根据垂直的定义可得出∠CFE=∠CDB=90°，进而可得出结论；
（2）根据BD∥EF可得出∠2=∠CBD，再由∠1=∠2得出GF∥BC，根据MD∥BC可知MD∥GF，据此可得出结论．
解答 证明：（1）∵BD⊥AC，EF⊥AC，
∴∠CFE=∠CDB=90°，
∴BD∥EF；
（2）∵BD∥EF，
∴∠2=∠CBD．
∵∠1=∠2，
∴∠CBD=∠1，
∴GF∥BC．
∵MD∥BC，
∴MD∥GF
∴∠AMD=∠AGF．
点评 本题考查的是平行线的性质，用到的知识点为：同位角相等，两直线平行．
练习册系列答案
相关题目
6．已知两点A（-5，y1），B（3，y2）均在抛物线y=ax2+bx+c（a≠0）上，点C（x0，y0）是该抛物线的顶点．若y1＜y2≤y0，则x0的取值范围是（ ）
| A． | -5≤x0-3 | B． | -5≤x0＜2 | C． | x0≥-5 | D． | -5≤x0＜-1 |
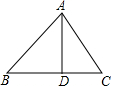如图，在△ABC中，AD⊥BC交BC于点D，若BC=14，AD=12，tan∠BAD=$\frac{3}{4}$，则DC的长为（ ）
11．在平面直角坐标系内有一点A的坐标是（-3，5），则点A到y轴的距离是（ ）
| A． | 3 | B． | 5 | C． | -3 | D． | -5 |
如图，矩形ABCD的对角线AC、BD交于点O，CE∥BD，DE∥AC．