题目内容
1.一个正数x的平方根是3a-4与8-a,则a和这个正数是多少?分析 根据一个正数有两个平方根,它们互为相反数得出3a-4+8-a=0,求出a,即可求出答案.
解答 解:根据一个正数有两个平方根,它们互为相反数得:3a-4+8-a=0,
即得:a=-2,
即3a-4=-10,
则这个正数=(-10)2=100.
点评 本题考查了平方根的应用,关键是得出关于x的方程,注意:一个正数有两个平方根,它们互为相反数.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
11.若分$\frac{x+y}{2xy}$中的x、y的值都变为原来的3倍,则此分式的值( )
| A. | 不变 | B. | 是原来的3倍 | C. | 是原来的$\frac{1}{3}$ | D. | 是原来的一半 |
9.观察下组数据,寻找规律:0、$\sqrt{3}$、$\sqrt{6}$、3、2$\sqrt{3}$、$\sqrt{15}$…那么第10个数据是( )
| A. | 2$\sqrt{6}$ | B. | 3$\sqrt{3}$ | C. | 7 | D. | $\sqrt{30}$ |
6.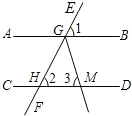 如图,直线EF分别与直线AB、CD相交于点G、H,已知∠1=∠2=70°,GM平分∠HGB交直线CD于点M,则∠3=( )
如图,直线EF分别与直线AB、CD相交于点G、H,已知∠1=∠2=70°,GM平分∠HGB交直线CD于点M,则∠3=( )
 如图,直线EF分别与直线AB、CD相交于点G、H,已知∠1=∠2=70°,GM平分∠HGB交直线CD于点M,则∠3=( )
如图,直线EF分别与直线AB、CD相交于点G、H,已知∠1=∠2=70°,GM平分∠HGB交直线CD于点M,则∠3=( )| A. | 50° | B. | 55° | C. | 60° | D. | 65° |
10.学校捐资购买了一批物资120吨打算支援山区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
(1)若全部物资都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?
(2)为了节省运费,该公司打算用甲、乙、丙三种车型同时参与运送,已知它们的总辆数为14辆,你能分别求出三种车型的辆数吗?此时的运费又是多少元?
| 车型 | 甲 | 乙 | 丙 |
| 汽车运载量(吨/辆) | 5 | 8 | 10 |
| 汽车运费(元/辆) | 400 | 500 | 600 |
(2)为了节省运费,该公司打算用甲、乙、丙三种车型同时参与运送,已知它们的总辆数为14辆,你能分别求出三种车型的辆数吗?此时的运费又是多少元?
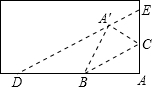 小王把一张矩形纸片沿BC折叠,顶点A落在点A′,再过点A′折叠使折痕DE∥BC,若AB=4,AC=3,则△ADE的面积是( )
小王把一张矩形纸片沿BC折叠,顶点A落在点A′,再过点A′折叠使折痕DE∥BC,若AB=4,AC=3,则△ADE的面积是( )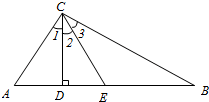 已知,如图,△ABC中,CD,CE分别是AB边上的高和中线,且∠1=∠2=∠3,求△ABC各内角的度数.
已知,如图,△ABC中,CD,CE分别是AB边上的高和中线,且∠1=∠2=∠3,求△ABC各内角的度数.