题目内容
3.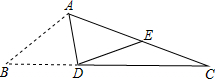 如图,AD是△ABC的角平分线,∠C=20°,AB+BD=AC,将△ABD沿AD所在直线翻折,点B在AC边上的落点记为点E,那么∠AED等于( )
如图,AD是△ABC的角平分线,∠C=20°,AB+BD=AC,将△ABD沿AD所在直线翻折,点B在AC边上的落点记为点E,那么∠AED等于( )| A. | 80° | B. | 60° | C. | 40° | D. | 30° |
分析 根据折叠的性质可得BD=DE,AB=AE,然后根据AC=AE+EC,AB+BD=AC,证得DE=EC,根据等边对等角以及三角形的外角的性质求解.
解答 解:根据折叠的性质可得BD=DE,AB=AE.
∵AC=AE+EC,AB+BD=AC,
∴DE=EC.
∴∠EDC=∠C=20°,
∴∠AED=∠EDC+∠C=40°.
故选C.
点评 本题考查了折叠的性质以及等腰三角形的性质、三角形的外角的性质,证明DE=EC是本题的关键.

练习册系列答案
相关题目
1.若关于x的不等式(3-m)x<3-m的解集为x>1,则m的取值范围是( )
| A. | m<0 | B. | m>0 | C. | m>3 | D. | m<3 |
8. 如图是一副三角尺叠放的示意图,则∠α的度数为( )
如图是一副三角尺叠放的示意图,则∠α的度数为( )
 如图是一副三角尺叠放的示意图,则∠α的度数为( )
如图是一副三角尺叠放的示意图,则∠α的度数为( )| A. | 75° | B. | 45° | C. | 30° | D. | 15° |
12.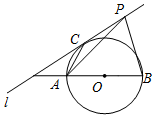 如图,直线l与以线段AB为直径的圆相切于点C,AB=6,AC=3,点P是直线l上一个动点.当∠APB的度数最大时,线段BP的长度为( )
如图,直线l与以线段AB为直径的圆相切于点C,AB=6,AC=3,点P是直线l上一个动点.当∠APB的度数最大时,线段BP的长度为( )
 如图,直线l与以线段AB为直径的圆相切于点C,AB=6,AC=3,点P是直线l上一个动点.当∠APB的度数最大时,线段BP的长度为( )
如图,直线l与以线段AB为直径的圆相切于点C,AB=6,AC=3,点P是直线l上一个动点.当∠APB的度数最大时,线段BP的长度为( )| A. | 6 | B. | $6\sqrt{3}$ | C. | 9 | D. | $3\sqrt{3}$ |




 在四边形ABCD中,AB=AD,请利用尺规在CD边上求作一点P,使得S△PAB=S△PAD,(保留作图痕迹,不写作法).
在四边形ABCD中,AB=AD,请利用尺规在CD边上求作一点P,使得S△PAB=S△PAD,(保留作图痕迹,不写作法). 如图所示,已知∠1+∠2=180°,∠B=∠3,DE和BC平行吗?如果平行,请说明理由.
如图所示,已知∠1+∠2=180°,∠B=∠3,DE和BC平行吗?如果平行,请说明理由.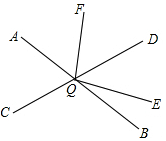 如图,直线AB、CD相交于点O,∠DOE:∠DOB=4:5,OF平分∠AOD,∠AOC=∠AOF-15°,则∠EOF的度数为105°.
如图,直线AB、CD相交于点O,∠DOE:∠DOB=4:5,OF平分∠AOD,∠AOC=∠AOF-15°,则∠EOF的度数为105°.