题目内容
19.解不等式组:$\left\{\begin{array}{l}{5x+2≥3(x-1)}\\{1-\frac{2x+5}{3}>x-2}\end{array}\right.$.分析 分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
解答 解:解不等式5x+2≥3(x-1),得:x≥-$\frac{5}{2}$,
解不等式1-$\frac{2x+5}{3}$>x-2,得:x<$\frac{4}{5}$,
故不等式组的解集为:-$\frac{5}{2}$≤x<$\frac{4}{5}$.
点评 本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
9.小明和小华参加社会实践活动,随机选择“打扫社区卫生”和“参加社会调查”其中一项,那么两人同时选择“参加社会调查”的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
7.2016年第一季度,我市“蓝天白云、繁星闪烁”天数持续增加,获得山东省环境空气质量生态补偿资金408万元,408万用科学记数法表示正确的是( )
| A. | 408×104 | B. | 4.08×104 | C. | 4.08×105 | D. | 4.08×106 |
14.下列函数中,满足y的值随x的值增大而增大的是( )
| A. | y=-2x | B. | y=3x-1 | C. | y=$\frac{1}{x}$ | D. | y=x2 |
4.若满足不等式20<5-2(2+2x)<50的最大整数解为a,最小整数解为b,则a+b之值为何?( )
| A. | -15 | B. | -16 | C. | -17 | D. | -18 |
11.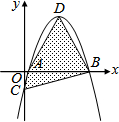 如图,坐标平面上,二次函数y=-x2+4x-k的图形与x轴交于A、B两点,与y轴交于C点,其顶点为D,且k>0.若△ABC与△ABD的面积比为1:4,则k值为何?( )
如图,坐标平面上,二次函数y=-x2+4x-k的图形与x轴交于A、B两点,与y轴交于C点,其顶点为D,且k>0.若△ABC与△ABD的面积比为1:4,则k值为何?( )
 如图,坐标平面上,二次函数y=-x2+4x-k的图形与x轴交于A、B两点,与y轴交于C点,其顶点为D,且k>0.若△ABC与△ABD的面积比为1:4,则k值为何?( )
如图,坐标平面上,二次函数y=-x2+4x-k的图形与x轴交于A、B两点,与y轴交于C点,其顶点为D,且k>0.若△ABC与△ABD的面积比为1:4,则k值为何?( )| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{4}{3}$ | D. | $\frac{4}{5}$ |
8.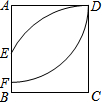 如图,以矩形ABCD的A为圆心,AD长为半径画弧,交AB于F点;再以C为圆心,CD长为半径画弧,交AB于E点.若AD=5,CD=$\frac{17}{3}$,则EF的长度为何?( )
如图,以矩形ABCD的A为圆心,AD长为半径画弧,交AB于F点;再以C为圆心,CD长为半径画弧,交AB于E点.若AD=5,CD=$\frac{17}{3}$,则EF的长度为何?( )
 如图,以矩形ABCD的A为圆心,AD长为半径画弧,交AB于F点;再以C为圆心,CD长为半径画弧,交AB于E点.若AD=5,CD=$\frac{17}{3}$,则EF的长度为何?( )
如图,以矩形ABCD的A为圆心,AD长为半径画弧,交AB于F点;再以C为圆心,CD长为半径画弧,交AB于E点.若AD=5,CD=$\frac{17}{3}$,则EF的长度为何?( )| A. | 2 | B. | 3 | C. | $\frac{2}{3}$ | D. | $\frac{7}{3}$ |
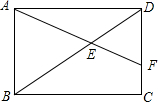 如图,矩形ABCD中,AB=$\sqrt{3}$,BC=$\sqrt{6}$,点E在对角线BD上,且BE=1.8,连接AE并延长交DC于点F,则$\frac{CF}{CD}$=$\frac{1}{3}$.
如图,矩形ABCD中,AB=$\sqrt{3}$,BC=$\sqrt{6}$,点E在对角线BD上,且BE=1.8,连接AE并延长交DC于点F,则$\frac{CF}{CD}$=$\frac{1}{3}$.