题目内容
12. 如图所示,如果△AOB与△AOD的周长之差为8,而AB:AD=3:2,那么?ABCD的周长( )
如图所示,如果△AOB与△AOD的周长之差为8,而AB:AD=3:2,那么?ABCD的周长( )| A. | 16 | B. | 24 | C. | 40 | D. | 80 |
分析 由四边形ABCD是平行四边形,△AOB的周长与△AOD的周长之差为8,可得AB-AD=8,又由AB:AD=3:2,即可求得AB与AD的长,继而求得答案.
解答 解:∵四边形ABCD是平行四边形,
∴OB=OD,AB=CD,AD=BC,
∵△AOB的周长与△AOD的周长之差为8,
∴(OA+OB+AB)-(OA+OD+AD)=AB-AD=8;
又∵AB:AD=3:2,
∴AB=24,AD=16.
∴?ABCD的周长=2(AB+AD)=80;
故选:D.
点评 此题考查了平行四边形的对角线互相平分的性质,三角形周长的计算;根据两个三角形的周长关系求出AB-AD=8是解决问题的突破口.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.张萌和小平两人打算各用一张正方形的纸片ABCD折出一个等边三角形,两人作法如下:张萌:如图1,将纸片对折得到折痕EF,沿点B翻折纸片,使点A落在EF上的点M处,连接CM,△BCM即为所求;小平:如图2,将纸片对折得到折痕EF,沿点B翻折纸片,使点C落在EF上的点M处,连接BM,△BCM即为所求,对于两人的作法,下列判断正确的是( )


| A. | 小平的作法正确,张萌的作法不正确 | |
| B. | 两人的作法都不正确 | |
| C. | 张萌的作法正确,小平的作法不正确 | |
| D. | 两人的作法都正确 |
20.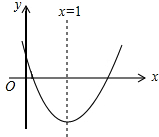 已知二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=1,下列结论中:①abc>0;②2a+b=0;③b2-4ac<0;④4a+2b+c>0;⑤3b<2c,其中正确的个数( )
已知二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=1,下列结论中:①abc>0;②2a+b=0;③b2-4ac<0;④4a+2b+c>0;⑤3b<2c,其中正确的个数( )
 已知二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=1,下列结论中:①abc>0;②2a+b=0;③b2-4ac<0;④4a+2b+c>0;⑤3b<2c,其中正确的个数( )
已知二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=1,下列结论中:①abc>0;②2a+b=0;③b2-4ac<0;④4a+2b+c>0;⑤3b<2c,其中正确的个数( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
17.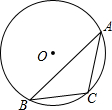 如图,△ABC内接于⊙O,BC=8,⊙O半径为5,则sinA的值为( )
如图,△ABC内接于⊙O,BC=8,⊙O半径为5,则sinA的值为( )
 如图,△ABC内接于⊙O,BC=8,⊙O半径为5,则sinA的值为( )
如图,△ABC内接于⊙O,BC=8,⊙O半径为5,则sinA的值为( )| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
4.在下列说法中,错误的是( )
| A. | 无限小数都是无理数 | B. | 实数与数轴上的点一一对应 | ||
| C. | 无理数都是无限小数 | D. | 带有根号的数不都是无理数 |
 已知:如图,点E、F分别为平行四边形ABCD的BC、AD边上的点,且∠1=∠2.求证:AE=FC.
已知:如图,点E、F分别为平行四边形ABCD的BC、AD边上的点,且∠1=∠2.求证:AE=FC. 在一次暖气管道的铺设工程中,由点A出发沿正西方向进行,在点A的南偏西55°的方向上有一个敬老院B,占地是以B为中心方圆100m的圆,当工程进行了200m后到达C处,此时B在C南偏西25°的方向上.请你根据题中所提供的信息计算并分析一下,工程继续进行下去,是否会穿越敬老院.
在一次暖气管道的铺设工程中,由点A出发沿正西方向进行,在点A的南偏西55°的方向上有一个敬老院B,占地是以B为中心方圆100m的圆,当工程进行了200m后到达C处,此时B在C南偏西25°的方向上.请你根据题中所提供的信息计算并分析一下,工程继续进行下去,是否会穿越敬老院.