题目内容
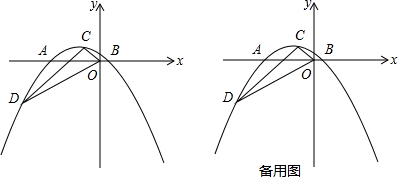
10.如图,顶点为C(-1,1)的抛物线经过点D(-5,-3),且与x轴交于点A、B两点(点B在点A的右侧).(1)求抛物线的解析式;
(2)抛物线上存在点Q,使得S△OAQ=$\frac{3}{2}$,求点Q的坐标;
(3)点M在抛物线上,点N在x轴上,且∠MNA=∠OCD,是否存在点M,使得△AMN与△OCD相似?若存在,直接写出点M的坐标;若不存在,说明理由.
分析 (1)用待定系数法求出抛物线解析式;
(2)先求出点A,B坐标,再用△OAQ的面积建立方程求出m,最后分两种情况建立方程求出点Q的坐标;
(3)先判断出△OCD是直角三角形,进而得出MN⊥x轴,设出点M坐标,表示出点N坐标,即可表示出AN,MN,借助(2)得出OC,CD,分两种情况用相似三角形的相似比建立方程求解即可得出结论.
解答 解:(1)∵抛物线顶点为C(-1,1),
∴设抛物线的解析式为y=a(x+1)2+1,
∵D(-5,-3)在抛物线上,
∴a(-5+1)2+1=-3,
∴a=-$\frac{1}{4}$,
∴抛物线的解析式为y=-$\frac{1}{4}$(x+1)2+1=-$\frac{1}{4}$x2-$\frac{1}{2}$x+$\frac{3}{4}$,
(2)由(1)知,抛物线的解析式为y=-$\frac{1}{4}$(x+1)2+1,
令y=0,∴0=-$\frac{1}{4}$(x+1)2+1,
∴x=1或x=-3,
∴A(-3,0),B(1,0),
∴OA=3,
设点Q的纵坐标为m,
∵S△OAQ=$\frac{3}{2}$,
∴$\frac{1}{2}$×3×|m|=$\frac{3}{2}$,
∴m=±1,
∵点Q在抛物线y=-$\frac{1}{4}$(x+1)2+1上,
当m=1时,-$\frac{1}{4}$(x+1)2+1=1,
∴x=-1,
∴Q(-1,1),
当m=-1时,-$\frac{1}{4}$(x+1)2+1=-1,
∴x=-1±2$\sqrt{2}$,
∴Q(-1+2$\sqrt{2}$,-1)或Q(-1-2$\sqrt{2}$,-1),
即:满足条件的Q的坐标为(-1,1)、(-1+2$\sqrt{2}$,-1)或(-1-2$\sqrt{2}$,-1).
(3)∵C(-1,1),D(-5,-3),
∴OC2=2,CD2=32,OD2=34,
∴OC2+CD2=OD2,
∴△OCD是直角三角形,
∴∠OCD=90°,
∴∠MNA=∠OCD=90°,
∵点M在抛物线上,点N在x轴上,
∴MN⊥x轴,
设M(n,-$\frac{1}{4}$n2-$\frac{1}{2}$n+$\frac{3}{4}$),
∴N(n,0),
∴AN=|n+3|,MN=|-$\frac{1}{4}$n2-$\frac{1}{2}$n+$\frac{3}{4}$|
∵△AMN与△OCD相似,
∴△AMN∽△ODC或△AMN∽△DOC,
①当△AMN∽△ODC时,
∴$\frac{MN}{CD}=\frac{AN}{OC}$,
∴$\frac{|-\frac{1}{4}{n}^{2}-\frac{1}{2}n+\frac{3}{4}|}{4\sqrt{2}}=\frac{|n+3|}{\sqrt{2}}$,
∴n=-3(舍)或n=17或n=-15,
∴M(17,-80)或(-15,-48),
②当△AMN∽△DOC时,
∴$\frac{MN}{OC}=\frac{AN}{CD}$,
∴$\frac{|-\frac{1}{4}{n}^{2}-\frac{1}{2}n+\frac{3}{4}|}{\sqrt{2}}=\frac{|n+3|}{4\sqrt{2}}$,
∴n=-3(舍)或n=2或n=0,
∴M(2,-$\frac{5}{4}$)或(0,$\frac{3}{4}$),
即:满足条件的点M的坐标为(17,-80)或(2,-$\frac{5}{4}$)或(0,$\frac{3}{4}$),或(-15,-48).
点评 此题是二次函数综合题,主要考查了待定系数法,三角形的面积公式,相似三角形的性质,解(1)的关键是掌握待定系数法,解(2)的关键是求出点Q的纵坐标,解(3)的关键是解绝对值方程,方程的思想是解决这类问题的关键,是一道中等难度的中考常考题.

 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案
 已知二次函数y=x2+2x+$\frac{k-1}{2}$与x轴有两个交点,且k为正整数.
已知二次函数y=x2+2x+$\frac{k-1}{2}$与x轴有两个交点,且k为正整数. 如图,∠AOC=∠COD=∠BOD,则OD平分∠BOC,OC平分∠AOD,∠AOB=$\frac{3}{2}$∠ADC=$\frac{3}{2}$∠BOC.
如图,∠AOC=∠COD=∠BOD,则OD平分∠BOC,OC平分∠AOD,∠AOB=$\frac{3}{2}$∠ADC=$\frac{3}{2}$∠BOC. 用两块完全相同的长方体搭成如图所示的几何体,从正面看得到的图形是( )
用两块完全相同的长方体搭成如图所示的几何体,从正面看得到的图形是( )



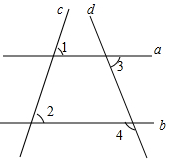 直线a、b、c、d的位置如图所示,如果∠1=58°,∠2=58°,∠3=70°,那么∠4等于110°.
直线a、b、c、d的位置如图所示,如果∠1=58°,∠2=58°,∠3=70°,那么∠4等于110°.